RRT and RRT* (Rapidly-Exploring Random Trees)
Reference
- https://msl.cs.illinois.edu/~lavalle/papers/Lav98c.pdf
- https://arxiv.org/pdf/1105.1186
- https://atsushisakai.github.io/PythonRobotics/modules/5_path_planning/rrt/rrt.html
RRT and RRT* (Rapidly-Exploring Random Trees)
Introduction
RRT는 대표적인 samplig-based algorithm 중 하나이다. RRT는 configuration space 내에서 무작위로 점을 선택하여 사용자가 정의한 action으로 공간을 빠르게 탐색해 나간다. search-based 알고리즘들에 비해 고차원에서도 빠르게 공간을 탐색 할 수 있다는 장점이 있다.
하지만 기본적인 RRT는 최적 경로를 보장해주지 않는다. 단순히 랜덤하게 점을 선택하여 앞으로 나아가고 있기 때문이다. 이를 어느정도 보안하기 위해 등장한 알고리즘이 RRT* 알고리즘이다. RRT* 는 choose parent 와 rewire 이동 cost를 최적화 시킨다.
Algorithm
RRT
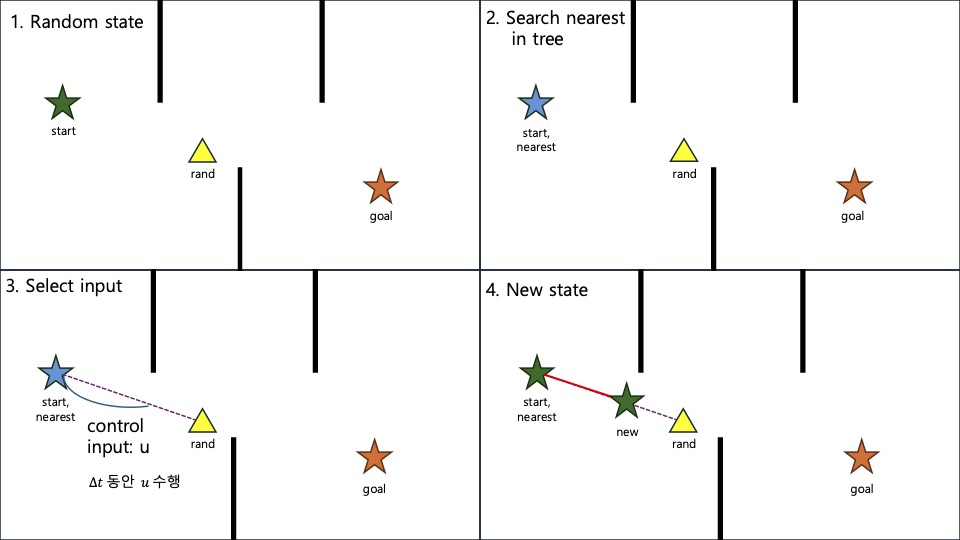
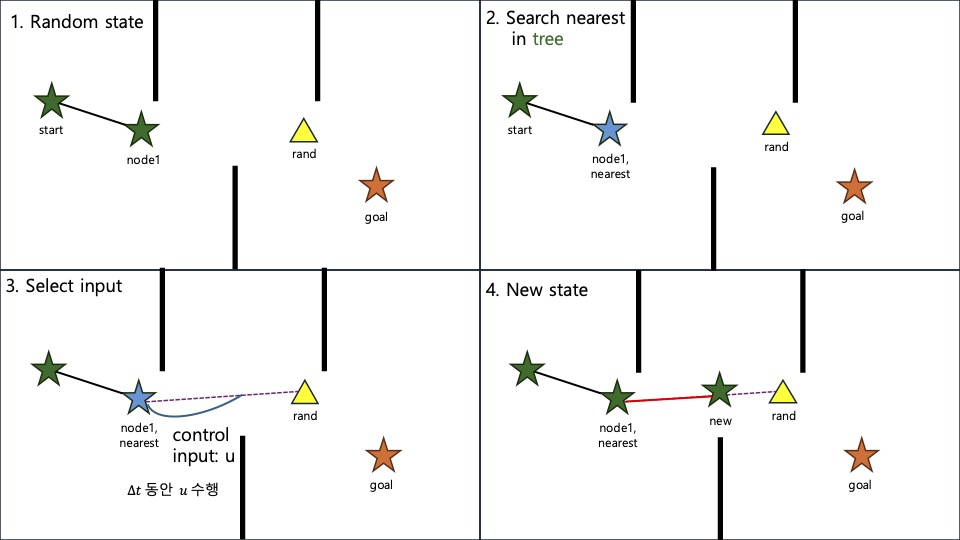
RRT는 약자 그대로 빠르게 공간을 탐색해 나가면서 트리를 구성해 나간다.
1
2
3
4
5
6
7
8
9
10
11
# RRT pseudo code
Algorithm 3: RRT
1: V ← {x_init}; E ← ∅
2: for i = 1, ..., n do
3: x_rand ← SampleFree_i
4: x_nearest ← Nearest(G = (V, E), x_rand)
5: x_new ← Steer(x_nearest, x_rand)
6: if ObstacleFree(x_nearest, x_new) then
7: V ← V ∪ {x_new};
E ← E ∪ {(x_nearest, x_new)}
8: return G = (V, E)
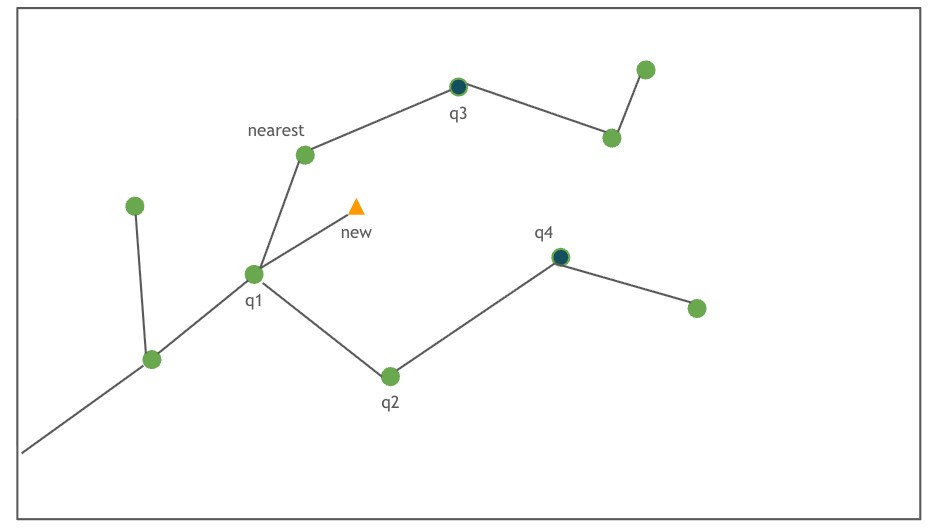
- 가장 먼저 시작점을 트리의 root node으로 생성한다.
- uniform random sample으로 점을 하나 뽑는다.
- 현재의 트리에서 random 점과 가장 가까운 점을 찾느다.
- 해당 점에서 random 점 까지 정의한 action으로 새로운 점을 찾고,
장애물과 충돌하지 않는다면 트리에 새로운 점을 추가하게 된다.
- 위 내용을 N회 만큼 정해둔 공간을 탐색한다.
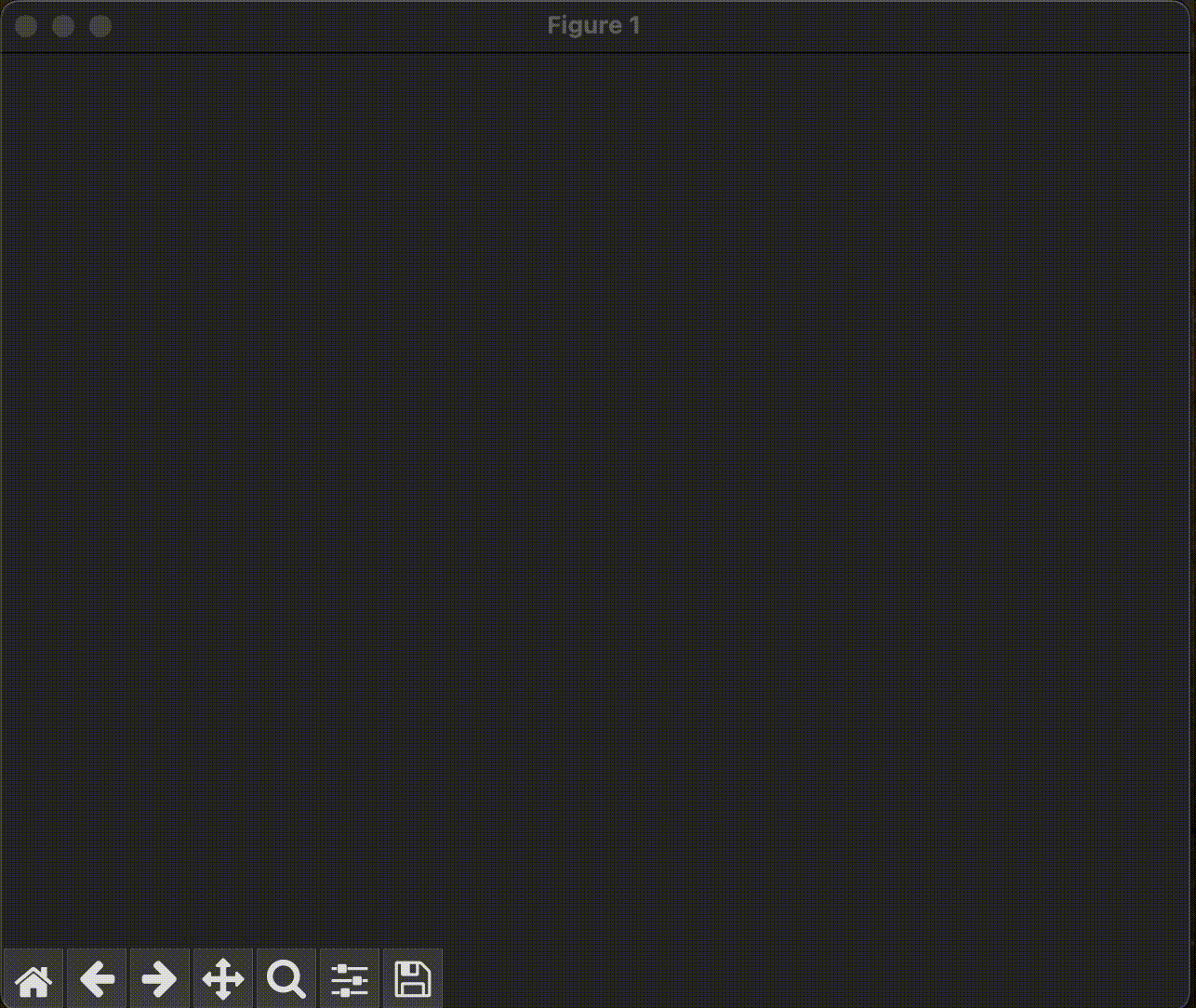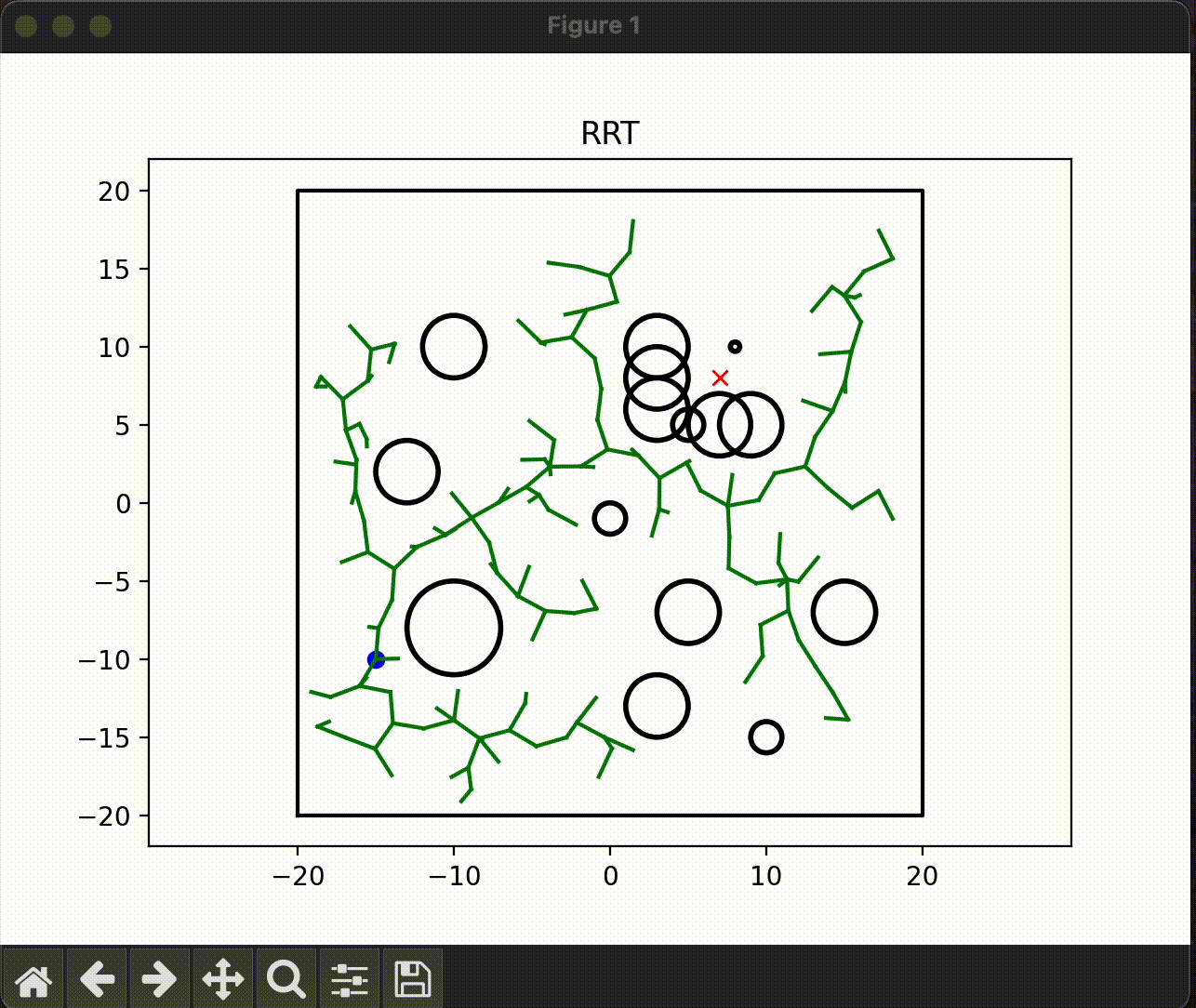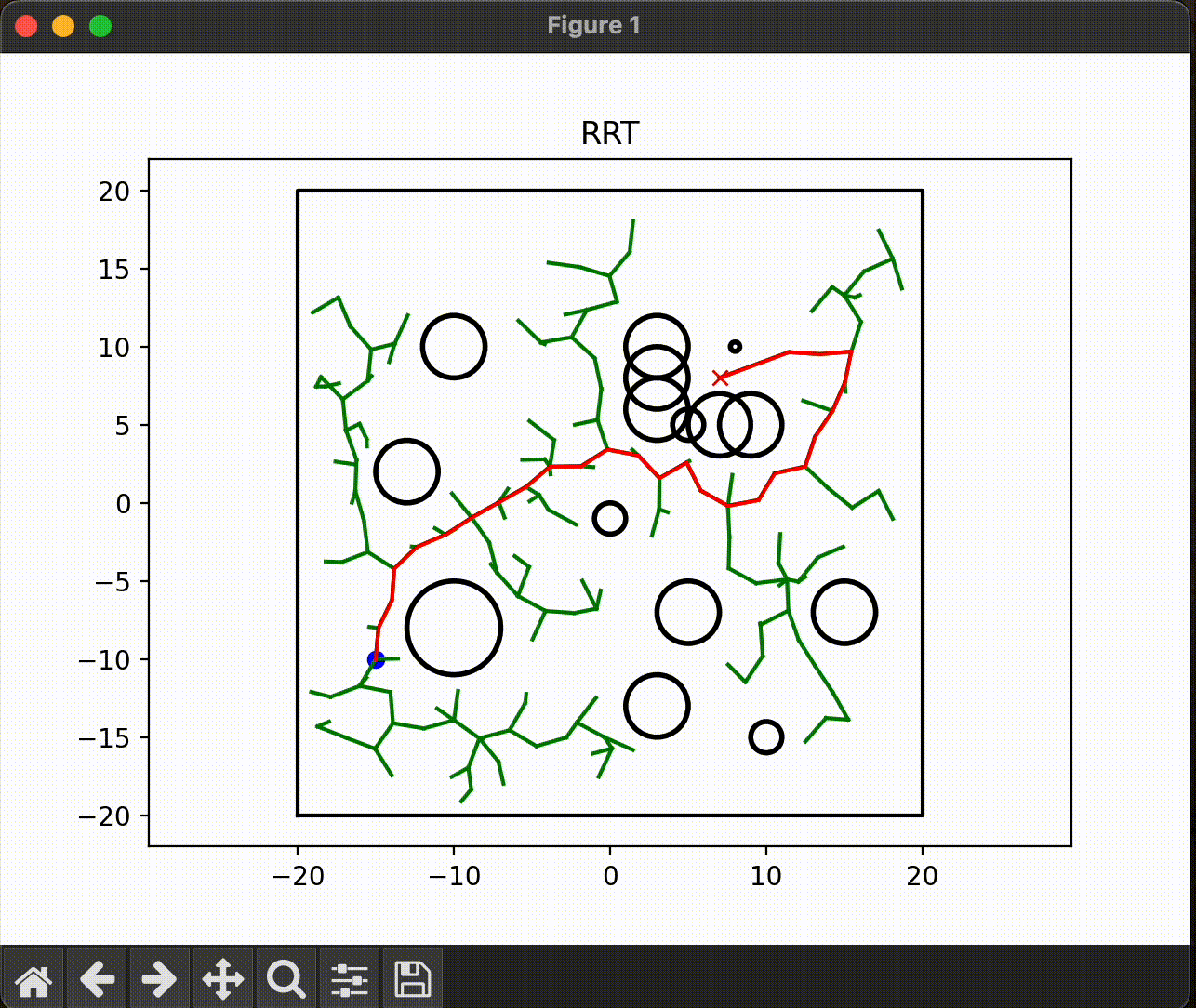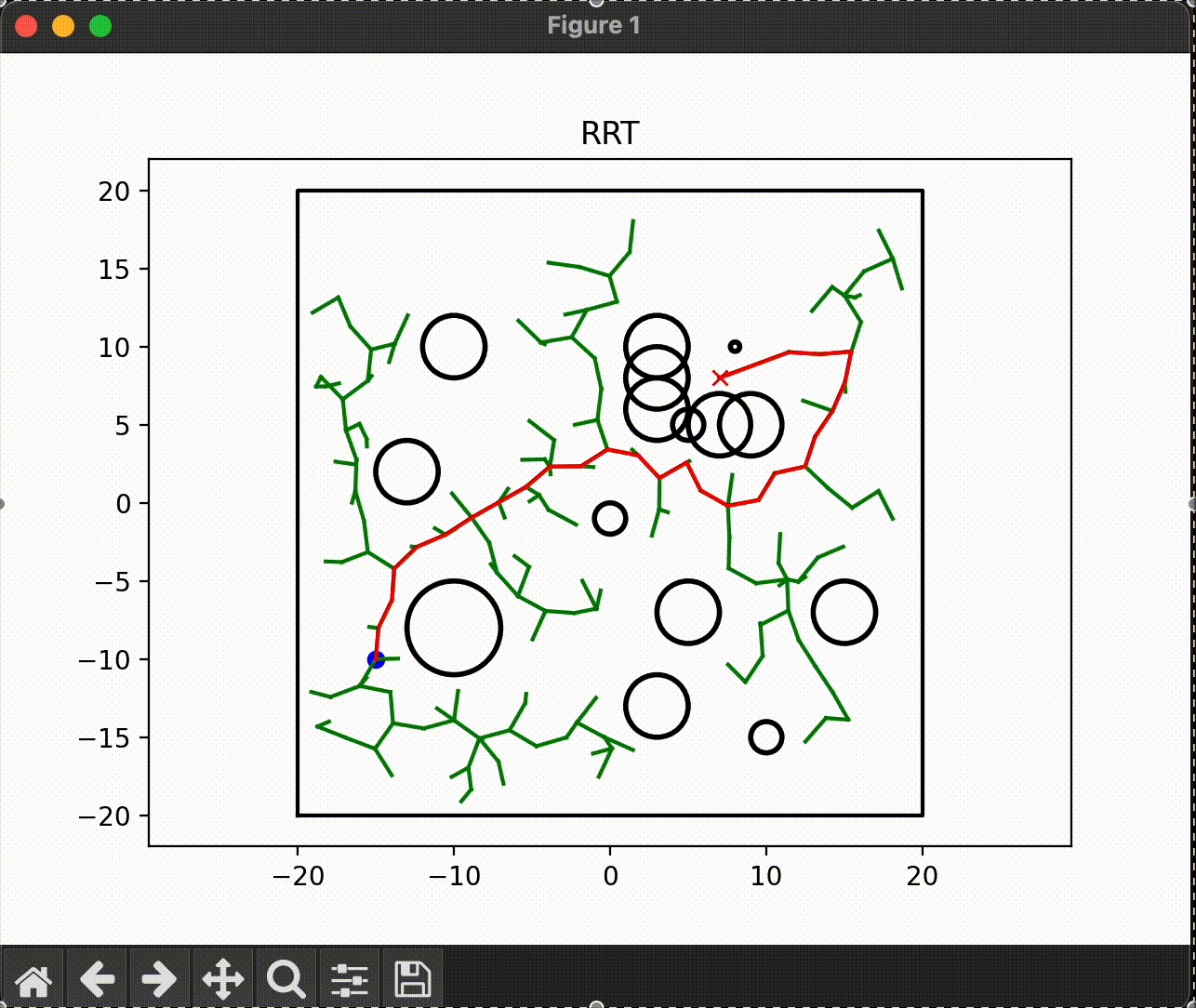
아래는 RRT 알고리즘으로 그려보았다.
RRT*
RRT* 는 RRT와 기본 구조는 같지만 choose parent 와 rewire 함수가 추가된 구조 이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# RRT* pseudo code
Algorithm 1: T = (V, E) ← RRT*(z_init)
1: T ← InitializeTree()
2: T ← InsertNode(∅, z_init, T)
3: for i = 1 to N do
4: z_rand ← Sample(i)
5: z_nearest ← Nearest(T, z_rand)
6: (x_new, u_new, T_new) ← Steer(z_nearest, z_rand)
7: if ObstacleFree(x_new) then
8: Z_near ← Near(T, z_new, |V|)
9: z_min ← ChooseParent(Z_near, z_nearest, z_new, x_new)
10: T ← InsertNode(z_min, z_new, T)
11: T ← ReWire(T, Z_near, z_min, z_new)
12: return T
Choose Parent
먼저 추가된 함수들중 choose_parent 를 먼저 확인해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
# ChooseParent pseudo code
Algorithm 2: z_min ← ChooseParent(Z_near, z_nearest, z_new, x_new)
1: z_min ← z_nearest
2: c_min ← Cost(z_nearest) + c(x_new)
3: for z_near ∈ Z_near do
4: (x', u', T') ← Steer(z_near, z_new)
5: if ObstacleFree(x') and x'(T') = z_new then
6: c' ← Cost(z_near) + c(x')
7: if c' < Cost(z_new) and c' < c_min then
8: z_min ← z_near
9: c_min ← c'
10: return z_min
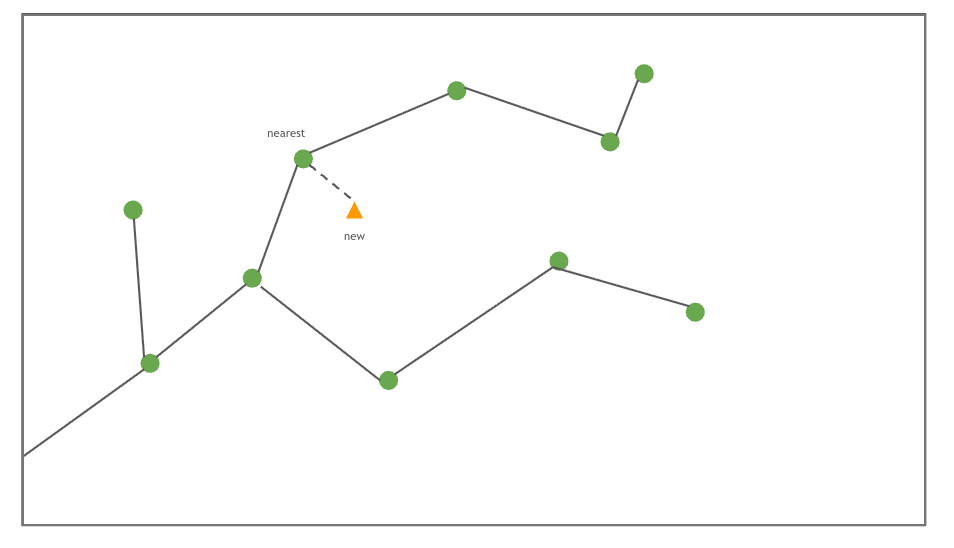
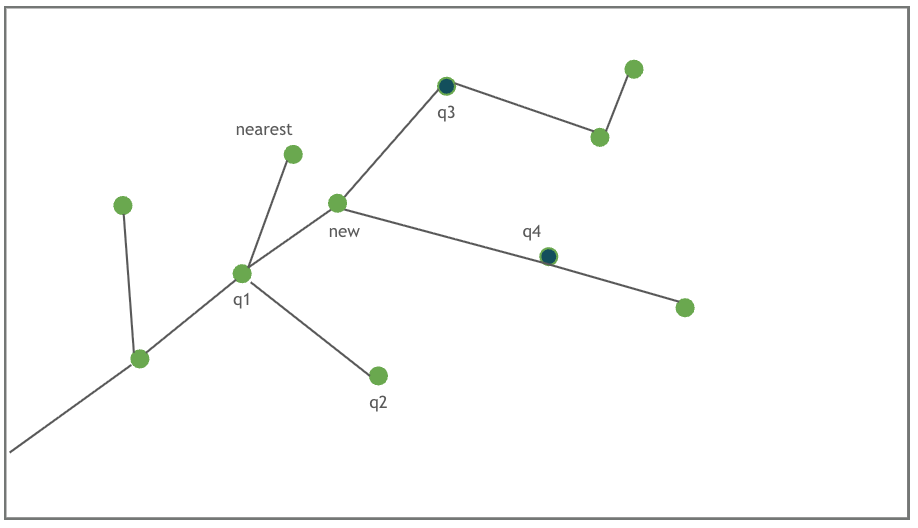
이전과 다르게 해당 함수에서는 단순하게 거리가 가까운 Node를 부모로 가지는것이 아닌
주변 Node 후보들 중에 새로운 Node로 갈 때 가장 적은 cost로 가는 Node를 확인하고,
가장 적은 cost를 가진 Node로 부모 Node를 교체한다.
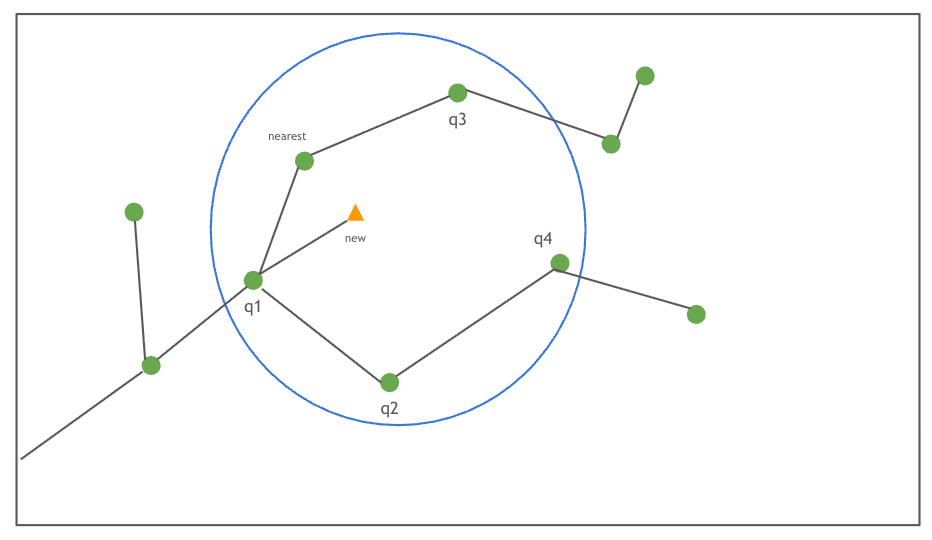
🌝 주변 후보들을 구하는 법
새 노드를 중점으로 하여 raduis = $\gamma \left(\frac{\log n}{n}\right)^{1/d}$ 를 가진 원안에 들오는 Node들이 parent의 후보들이다.
$\gamma$ = 내가 설정하는 상수, $n$ = 현재 트리의 노드 수, $d$ = 상태공간의 차원
Rewire
다음은 rewire 함수이다.
1
2
3
4
5
6
7
8
9
# Rewire pseudo code
Algorithm 3: T ← ReWire(T, Z_near, z_min, z_new)
1: for z_near ∈ Z_near \ {z_min} do
2: (x', u', T') ← Steer(z_new, z_near)
3: if ObstacleFree(x') and x'(T') = z_near and
4: Cost(z_new) + c(x') < Cost(z_near) then
5: T ← ReConnect(z_new, z_near, T)
6: return T
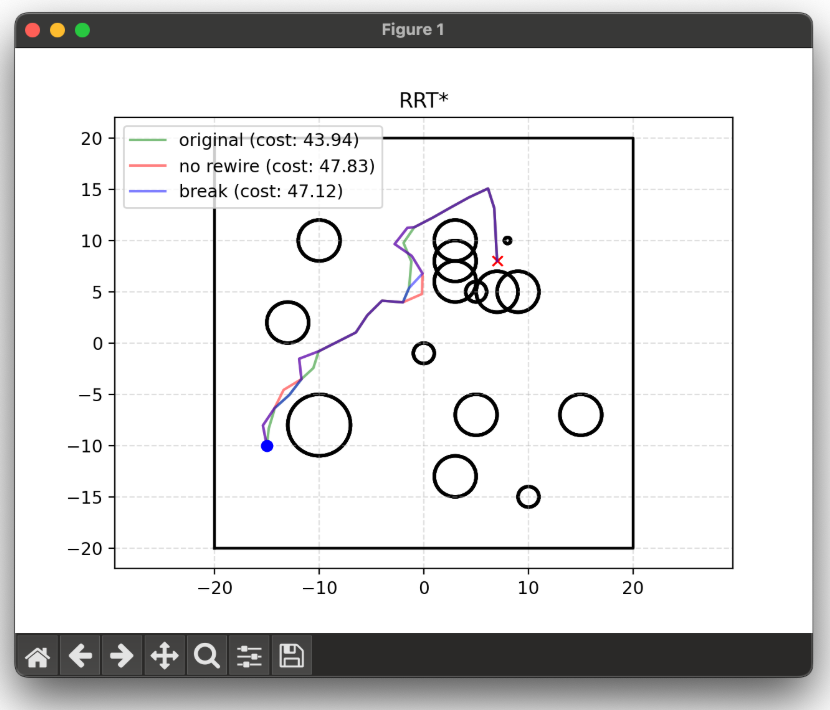
rewire 함수는 변경된 parent를 기반으로 더 적은 cost로 다른 주변 노드로 갈 수 있다면 다시 트리 연결을 구성해주는 함수이다.
이렇게 rewire 함수를 반복적으로 계속해서 수행하다보면 최적경로와 RRT*의 경로 결과가 점점 가까워진다.
위 함수들때문에 RRT*는 해당 함수들을 얼마나 많이 반복하느냐에 따라 결과가 달라진다.
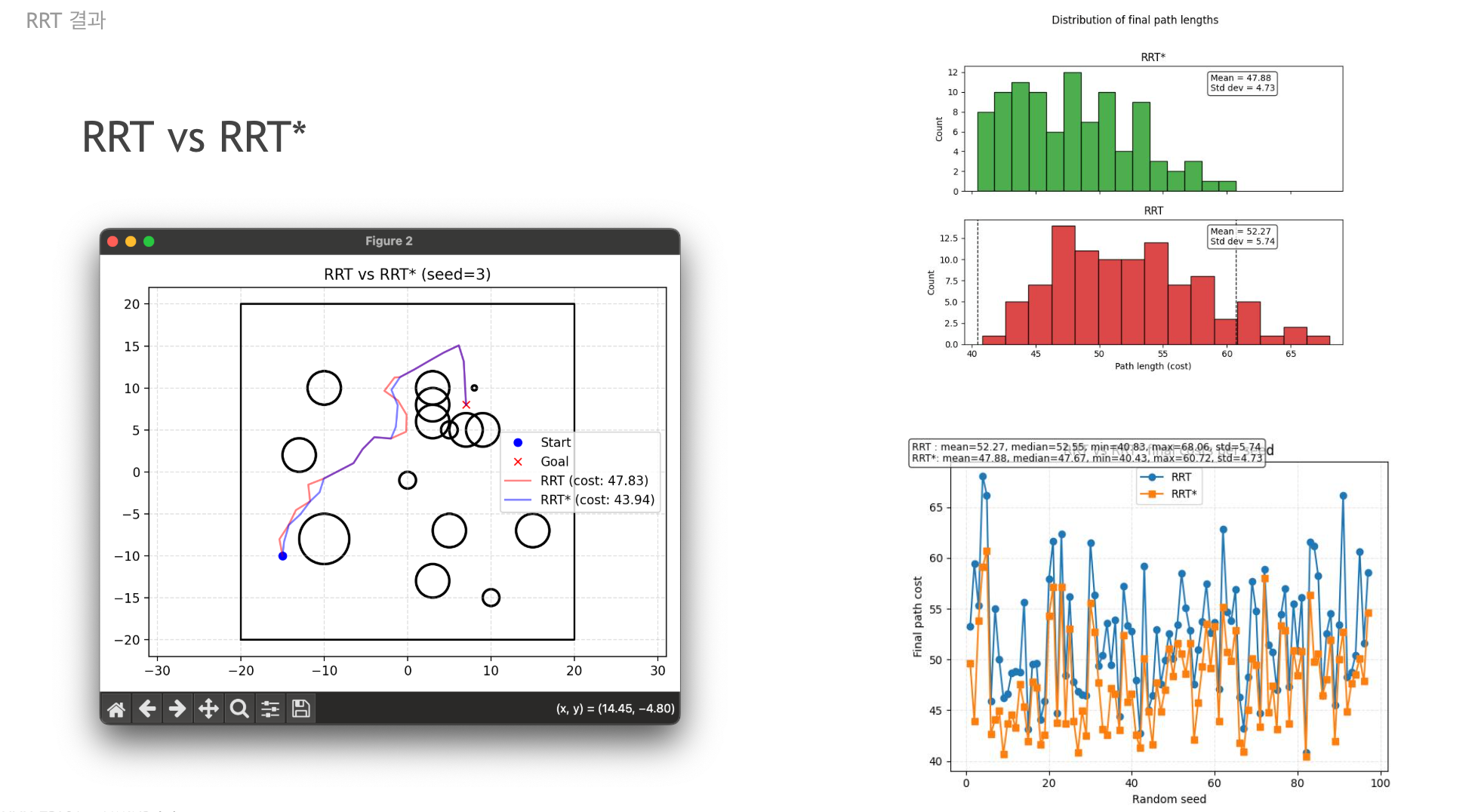
아래 결과에서 rewire를 했을때, 안했을때
도착점에 도착하면 멈출때를 비교해보았다.
Result
RRT (normal, dubins)
RRT*