Pure Pursuit
Reference
- https://www.mathworks.com/help/nav/ug/pure-pursuit-controller.html
- https://koreatech-kroad.github.io/Pure-Pursuit-&-Stanely
- https://dionysaurus.tistory.com/293
Pure Pursuit
Introduction
Pure Pursuit은 간단한 path tracking 알고리즘으로 사용된다.
보통 횡방향에 대한 제어를 하기위해 해당 알고리즘을 사용하게 된다.
차량의 후륜축의 중심점을 기준으로 목표점까지의 거리 (LookAhead Distance = LD)와
차량의 모델을 간소화한 Bicycle model을 사용하여 steer angle을 제어하게 된다.
Method
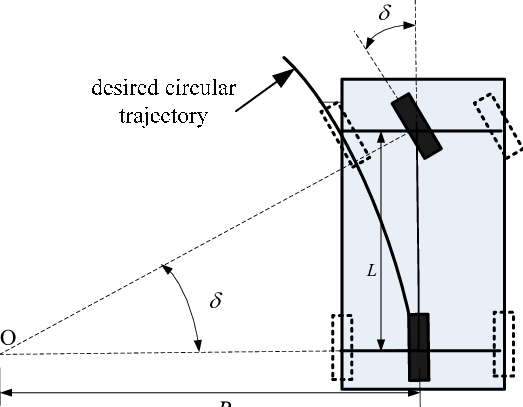
출처: https://www.researchgate.net/figure/Equivalent-bicycle-model-of-Ackerman-steered-vehicle_fig2_261345739
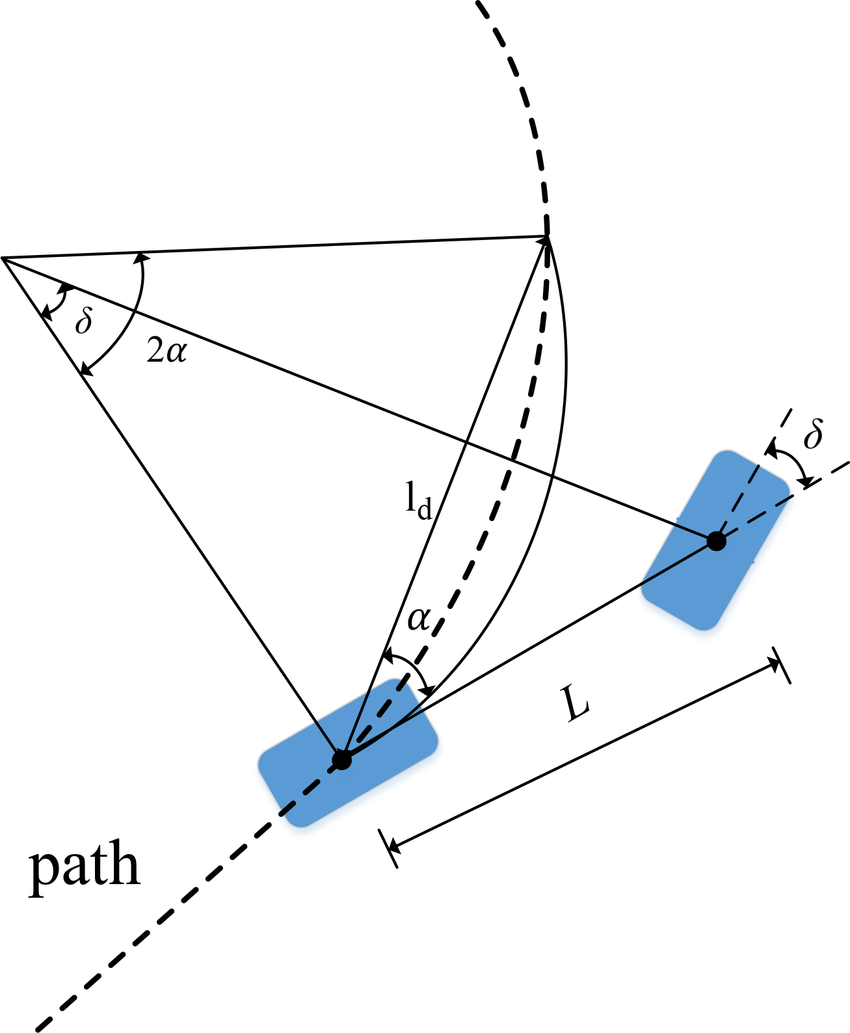
위 사진에서 볼 수 있는 것 처럼
- L : Wheel base
- δ : 조향각
- Ld : 후륜축 중심과 목표 지점 사이의 거리
- α : 차향의 heading과 Ld 사이의 각도
- R : 차량의 회전반경
으로 구성되어 있다.
Steering angle 계산
삼각형의 성질을 이용해면 $\delta$ 를 구해 낼 수 있다.
\(tan(\delta) = \frac{L}{R}\)
\(\therefore\; \delta = tan^{-1}(\frac{L}{R})\)
으로 표현할 수 있다.
pure pursuit을 이용한 steer angle 구하기
위의 steering angle을 계산하는 방식을 이용해서 pure pursuit으로 조향할 angle을 구할 수 있다.
먼저 원점에서 Ld 선분 위로 수선의 발을 내리게 되면 해당 삼각형은 이등변삼각형이기 때문에 $2\alpha$가 만으로 나뉘게 된다.
그럼 $\alpha$를 이용해 반지름 R을 구할 수 있게 된다. $d_{la}$ = 길이가 Ld인 선분
\(sin(\alpha) = \frac{\frac{d_{la}}{2}}{R}\)
\(\therefore\;R = \frac{2sin(\alpha)}{d_{la}}\)
위의 식에 R을 대입하여 적게 되면
우리가 구할 angle은 다음과 같이 표현할 수 있다.
\(\delta = \tan^{-1}\!\left( \frac{2L\sin \alpha}{d_{la}}\right)\)
그럼 이제 $\alpha$ 에 대한 정보만 알면 angle을 완전히 구할 수 있다.
$\alpha$는 다음과 같이 표현된다.
\(\alpha = \tan^{-1}(\frac{dy}{dx}) - yaw_{curr}\)
LookAhead의 따른 변화
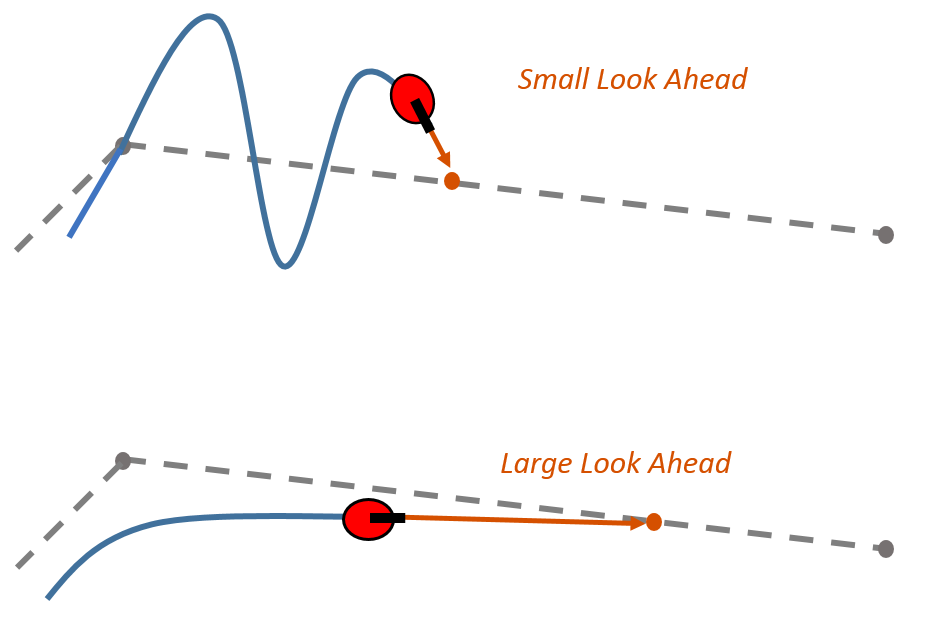
Small Look-ahead
- 전방 주시거리가 짧으면 이동체가 쁠게 경로를 향해 이동하려고 한다.
- 하지만, 빠르게 도달하기 위해 경로의 진동이 심해질 수 있다. (각을 크게 주기 때문)
Large Look-ahead
- 경로가 급격하게 변하는 곡률에서는 경로를 정확하게 따라기 못하는 단점이 존재한다.
- 하지만, 진동이 줄어들고 조금 더 부드럽게 추종할 수 있다.
LookAhead 설정
속도에 비례하여 look ahead를 설정하게 되면 비교적 횡방향 제어가 잘되는 것을 확인할 수 있다.
Result
해당 영상은 횡방향 (Pure Pursuit), 종방향 (PID control)을 한 시뮬레이션 영상이다.
