Optimal Trajectories in a Frenet Frame

Reference

• Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame, ICRA, 2010
• Optimal trajectories for time-critical street scenarios using discretized terminal manifolds, IJRR, 2011
• https://github.com/DongchanKim05/planning/tree/main/python/polynomial
• https://github.com/AtsushiSakai/PythonRobotics/tree/master/PathPlanning/FrenetOptimalTrajectory

Optimal Trajectories in a Frenet Frame

Introduction

Frenet frame 상에서 가속도의 변화량인 jerk를 가장 최소화하는 polynomial을 이용해 안전하고 편안한 주행 경로를 만들어낸다. frenet frame을 사용하면 복잡한 도로 환경에서도 문제를 단순화할 수 있으며, 종방향과 횡방향을 나눠 경로를 생성하기 용이해진다. 이런 특성은 실제 사람이 운전하는 방식과 유사하게 주행 경로를 만들 수 있다.

Frenet Frame

Frenet Frame 이란?

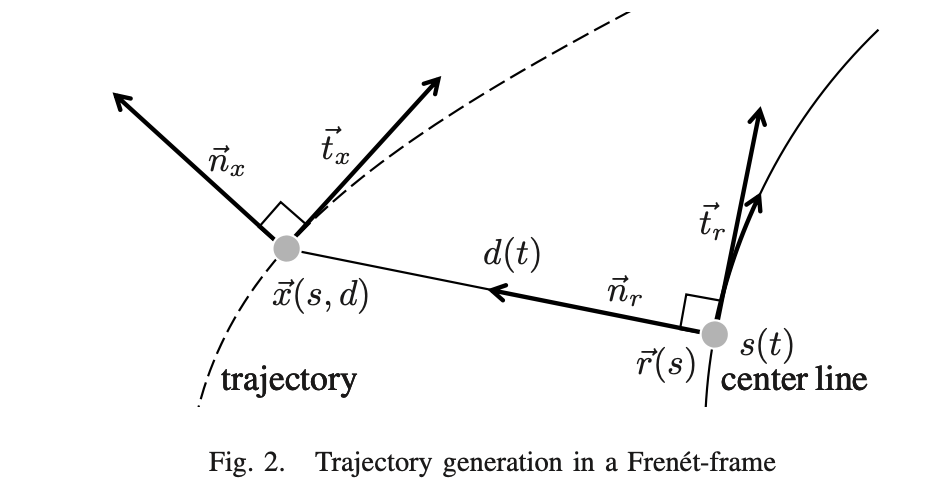
Frenet frame은 도로의 중심선을 기준으로 정의되는 좌표계라고 할 수 있다.
차량의 위치를 도로 중심선을 따라간 거리의 종방향 좌표 s, 중심선에서의 수직거리인 횡방향 좌표 d로 표현한다.

Cartesian coordinate은 Frenet coordinate으로 다음과 같이 표현된다. \(\mathbf{x}(s(t), d(t)) = \mathbf{r}(s(t)) + d(t)\,\mathbf{n}_r(s(t))\)

• $\mathbf{r}(s)$: 도로 중심선 상의 점
• $\mathbf{n}_r(s)$: 중심선에서의 법선 벡터
• $s$: 중심선을 따라간 arc length
• $d$: 중심선으로부터의 횡방향 거리

출처: "Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame", ICRA, 2010.

출처: "A Hierarchical Motion Planning Framework for Autonomous Driving in Structured Highway Environments," IEEE Access, 2022.

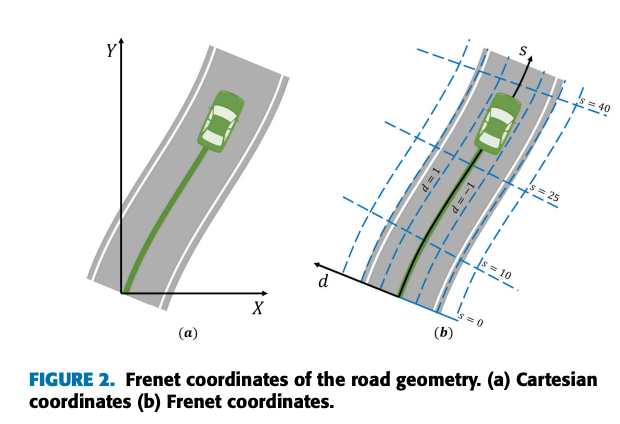
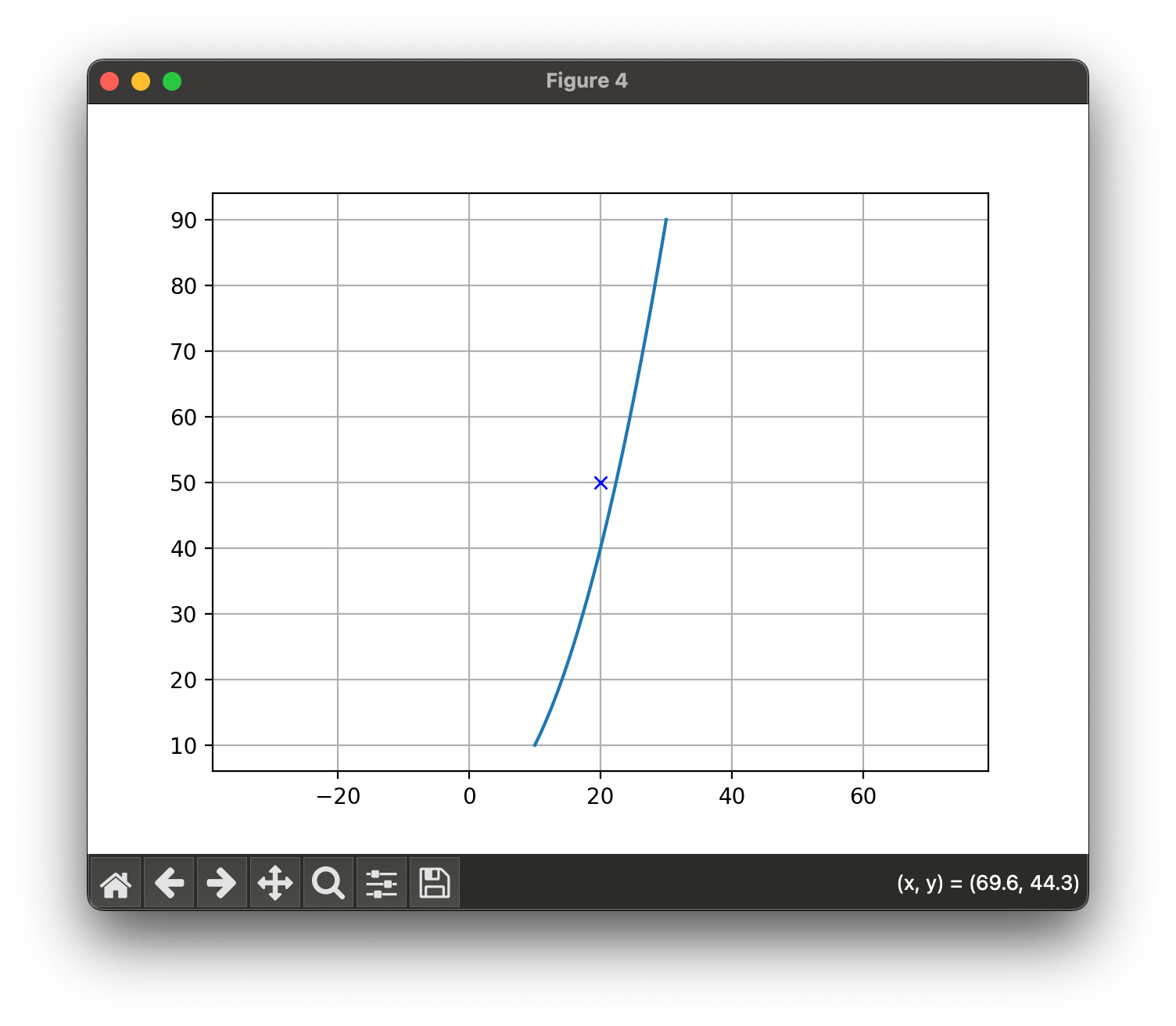
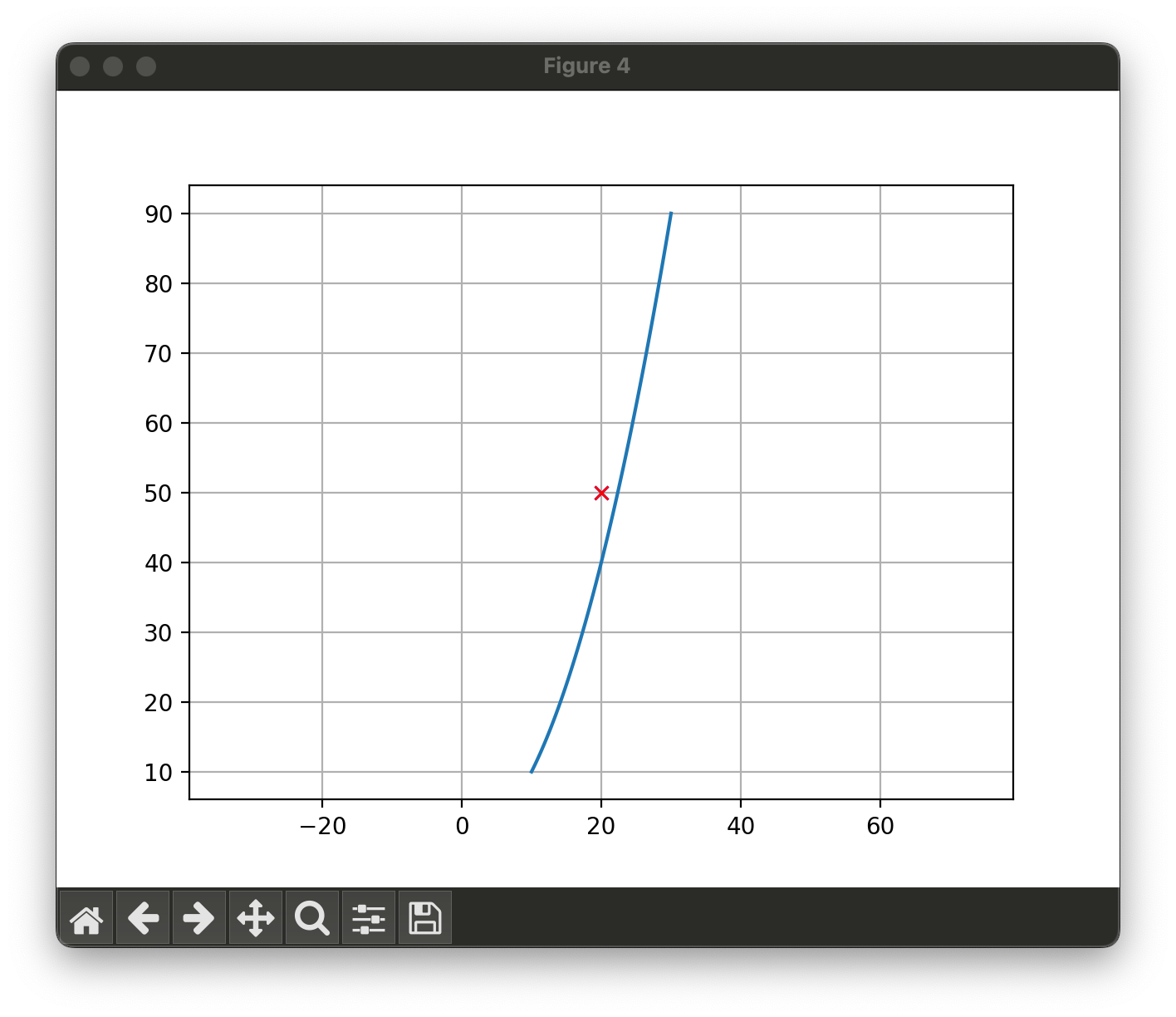
Frenet Frame으로의 변환

나는 조금 다른 방식으로 변환하였다.

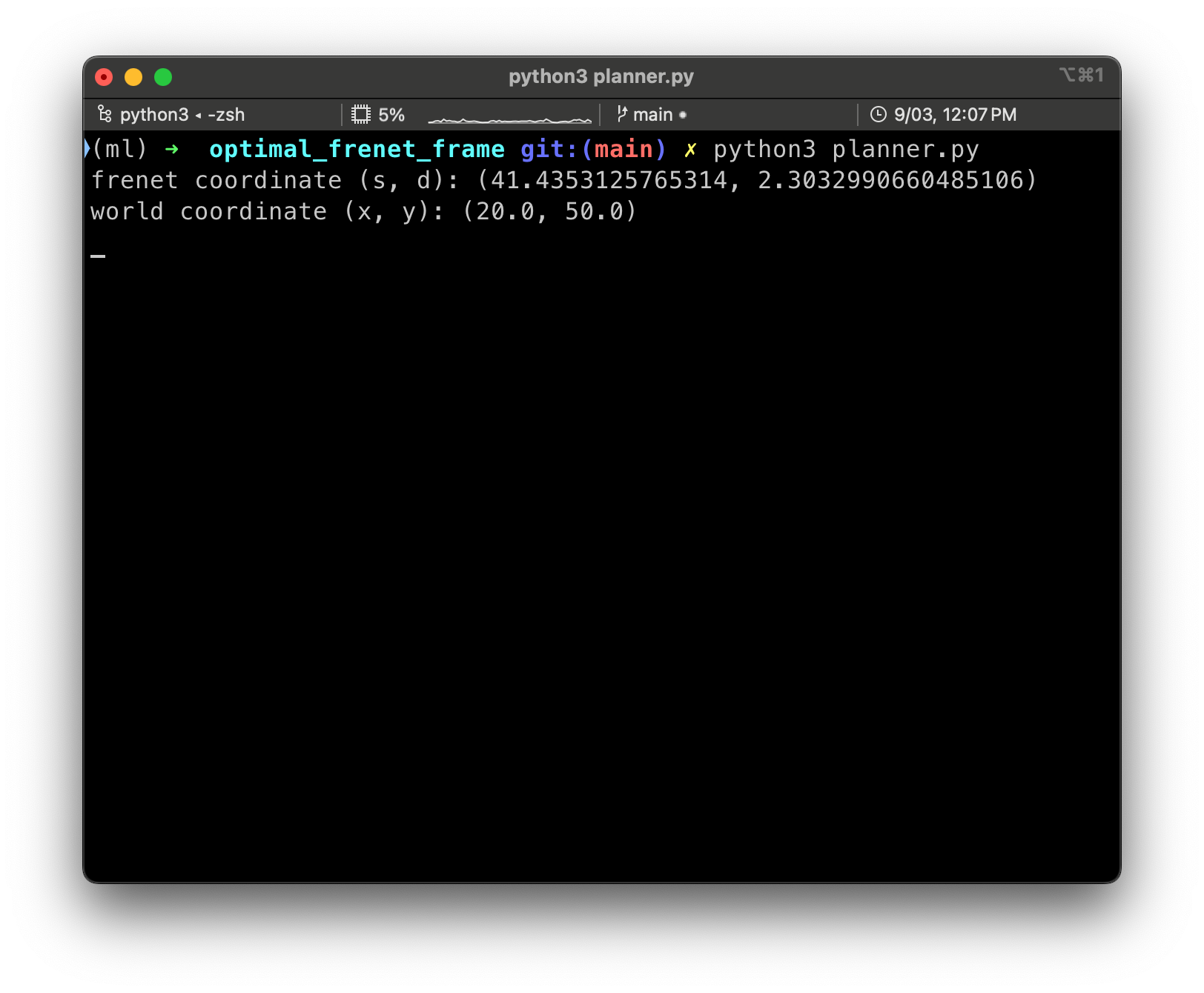
cartesian → frenet

1. 차량 위치 $(x, y)$와 중심선 waypoint 집합 (frenet s의 집합) 사이의 거리를 계산하여 가장 가까운 waypoint를 찾는다.
2. 내적을 이용해 waypoint가 차량 앞에 있는지 확인한 뒤, 현재 segment 방향 벡터 $\mathbf{t}$를 구한다.
3. 차량 위치 벡터를 segment에 직교 투영하여 projection 벡터 $\mathbf{e}_{\text{proj}}$를 얻는다.
4. lateral offset $d$는 실제 위치와 projection 차이로 계산하며, 외적 부호로 좌/우 방향을 판별한다.
5. 종방향 좌표 $s$는 이전 waypoint까지의 누적 arc length에 projection 길이를 더해 계산한다.

frenet → cartesian

1. 선택된 waypoint 구간을 중심선으로 두고, arc length $s$를 따라간 점 $\mathbf{r}(s)$와 해당 segment 방향의 단위 법선 벡터 $\mathbf{n}_r(s)$를 구한다.
2. 차량의 Cartesian 좌표는 다음과 같이 계산한다. $\mathbf{x}(s, d) = \mathbf{r}(s) + d \,\mathbf{n}_r(s)$
3. 필요하다면 heading, 곡률 $\kappa$, 속도 $v$, 가속도 $a$도 Frenet 상태 변수($s’, s’’, d’, d’’$)로부터 변환할 수 있다.

Example

현재 world 좌표 위치	frenet → world	변환 결과

Generate Trajectory with Polynomial

우리의 목적인 jerk ( $J_t(p(t)) := \int_{t_0}^{t_1} \dddot{p}^{\,2}(\tau) \, d\tau$ ) 를 최소화하는 다항식은 상황에 따라 4차 혹은 5차 다항식이다.
다항식을 구하기 위해 우리는 최소 6개의 정보 (4차일때는 5개)가 필요하다. 따라서 다음과 같은 정보를 이용하게 된다.
\(q(t) = c_0 + c_1 t + c_2 t^2 + c_3 t^3 + c_4 t^4 + c_5 t^5\)

초기 조건 (위치, 속도, 가속도), 종단 조건 (위치, 속도, 가속도) :

\[q(0) = q_i^0, \quad \dot{q}(0) = q_i^1, \quad \ddot{q}(0) = q_i^2\] \[q(T) = q_t^0, \quad \dot{q}(T) = q_t^1, \quad \ddot{q}(T) = q_t^2\]

다항식 계수 구하기

아래의 행렬 계산을 이용하여 다항식의 계수들을 구할 수 있다. (4차의 경우 조금 변형하면된다.)

\[\begin{bmatrix} q_t^0 \\ q_t^1 \\ q_t^2 \end{bmatrix} = \underbrace{\begin{bmatrix} 1 & T & T^2 \\ 0 & 1 & 2T \\ 0 & 0 & 2 \end{bmatrix}}_{M_1} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \end{bmatrix} + \underbrace{\begin{bmatrix} T^3 & T^4 & T^5 \\ 3T^2 & 4T^3 & 5T^4 \\ 6T & 12T^2 & 20T^3 \end{bmatrix}}_{M_2} \begin{bmatrix} c_3 \\ c_4 \\ c_5 \end{bmatrix}\] \[c_0 = q_i^0, \quad c_1 = q_i^1, \quad c_2 = \tfrac{1}{2} q_i^2\] \[\begin{bmatrix} c_3 \\ c_4 \\ c_5 \end{bmatrix} = M_2^{-1} \left( \begin{bmatrix} q_t^0 \\ q_t^1 \\ q_t^2 \end{bmatrix} - M_1 \begin{bmatrix} c_0 \\ c_1 \\ c_2 \end{bmatrix} \right)\]

lateral trajectory

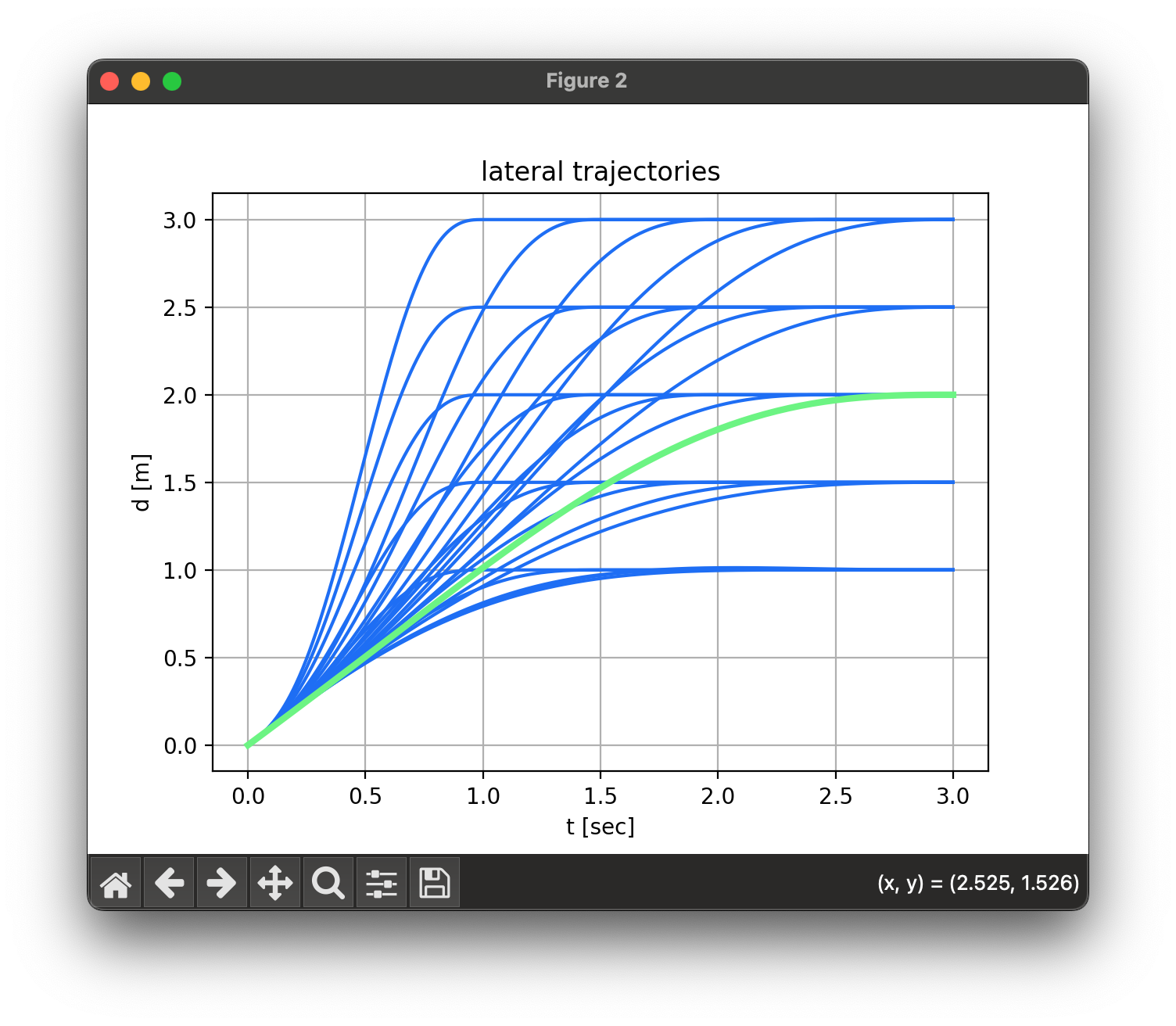
횡방향 경로의 경우 5차 다항식을 사용하여 경로를 생성한다. 경로에 대한 cost는 다음과 같이 계산한다. \(C_d = k_j J_t(d(t)) + k_t T + k_d d_1^2\)

하지만, 저속의 경우 차량의 non-holonomic 제약이 커지기 때문에 d를 s에 종속하여 계산하는 식을 이용하게 된다. \(C_d = k_j J_t(d(s)) + k_t S + k_d d_1^2\)

종단 조건은 [목표 횡방향 위치 집합, 0, 0] 으로 설정한다.

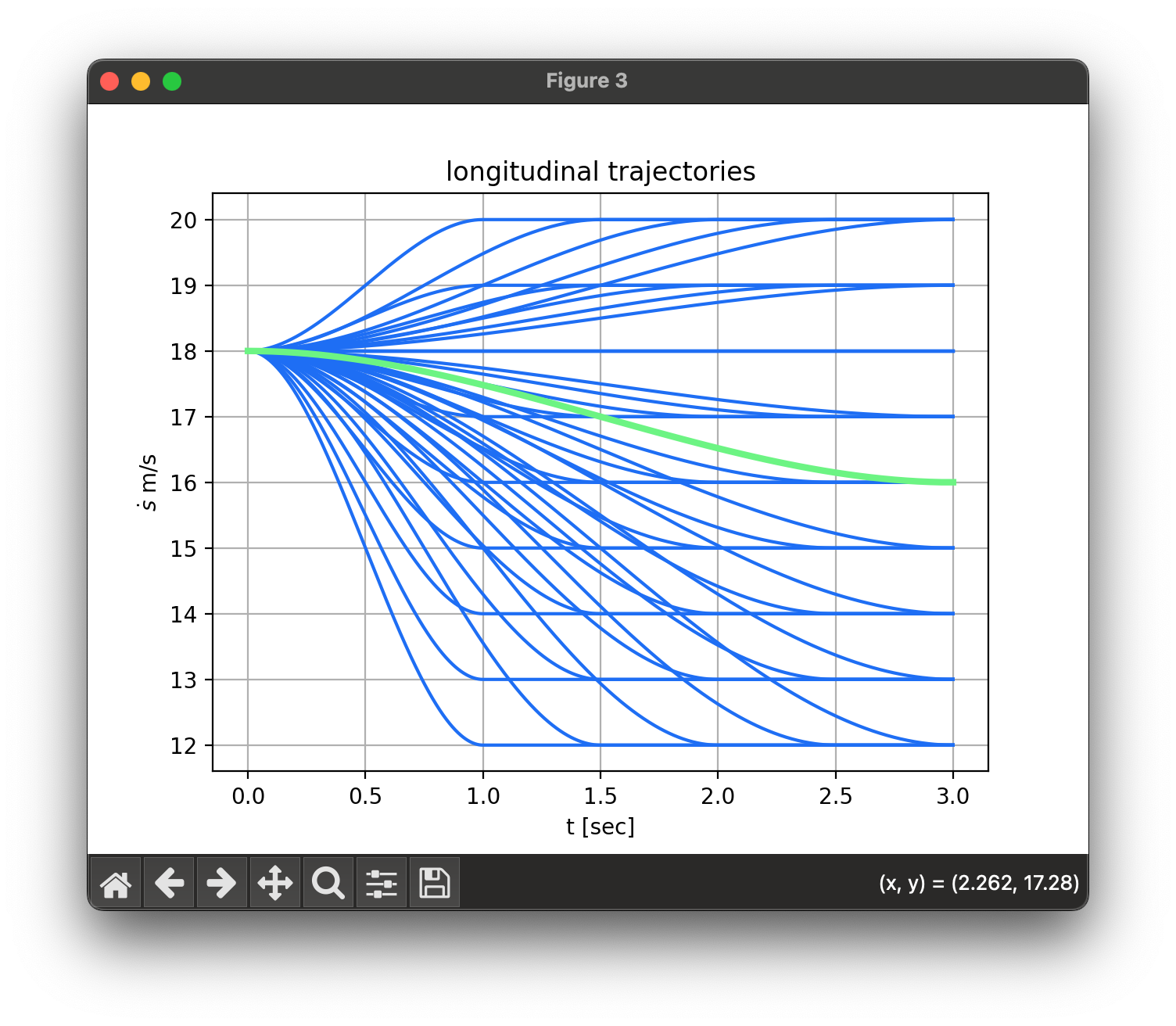
longitudinal trajectory

velocity keeping

속도 유지를 위한 경우에 4차 다항식을 사용하게 되는데, 종단 위치 여부는 신경 쓰지 않아도 되는 정보이기 때문에 해당 정보를 제외하고 5개의 정보만을 이용해 4차 다항식을 구하여 경로를 생성한다.
속도 유지 경로에 대한 cost는 다음과 같이 계산한다. \(C_v = k_j J_t(s(t)) + k_t T + k_s \left[\dot{s}_1 - \dot{s}_d\right]^2\)

following, merging and stopping

속도 유지외의 경우들은 모두 5차 다항식을 사용한다.
경로에 대한 cost는 다음과 같이 계산한다. \(C_t = k_j J_t + k_t T + k_s \left[s_1 - s_d\right]^2\)

종단 조건 설정

• following : $\left[\, s_\text{lv}(T) - (D_0 + \tau \dot{s}\text{lv}(T)), \; \dot{s}\text{lv}(T), \; \ddot{s}_\text{lv}(T) \,\right]$

  → 앞차 위치 기준, 일정 시간 간격 $\tau$와 최소 거리 $D_0$ 유지.

• merging : $\left[\, \tfrac{1}{2}(s_a(T) + s_b(T)), \;\; \tfrac{1}{2}(\dot{s}_a(T) + \dot{s}_b(T)), \;\; 0 \,\right]$
• stopping : $[\, s_\text{stop}, \; 0, \; 0 \,]$

Example

횡방향 경로 생성 (목표 d: 2)	종방향 경로 생성 (4차 다항식 사용, 목표 𝑠˙=16)

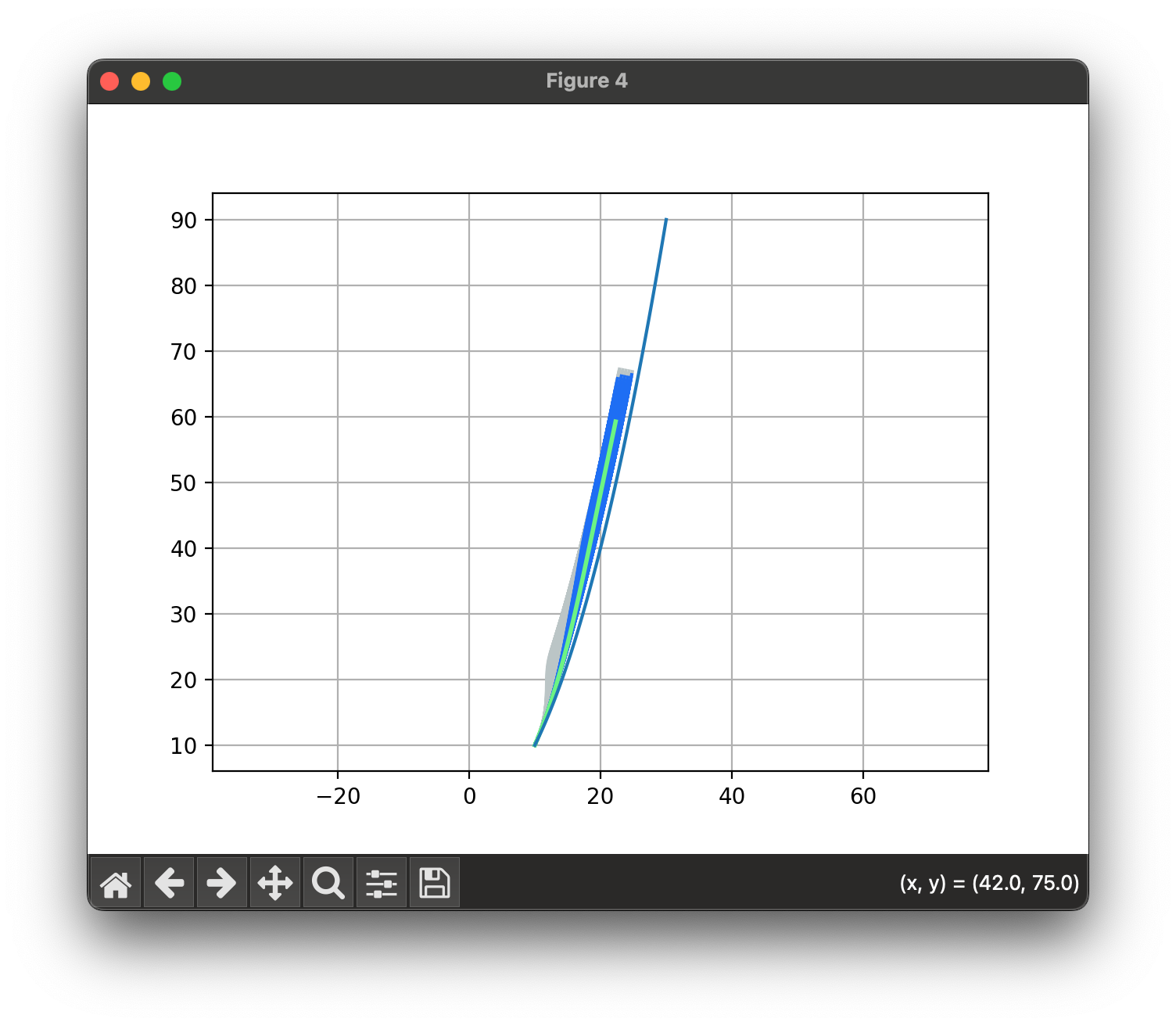
Combining lateral and longitudinal trajectories

• 유효한 경로 검사 조건
• 최대 속도 초과 여부
• 최대 가속도(ACC_MAX) 초과 여부
• 최대 곡률(K_MAX) 초과 여부
• 장애물과 충돌 여부

위 제약들을 검사한 후 비용함수를 이용해 비용이 가장 작은 optimal trajectory를 선택하게 된다.

Cost Function : $C_{\text{tot}} = k_{\text{lat}} C_{\text{lat}} + k_{\text{lon}} C_{\text{lon}}$

Select mode

velocity keeping, following, merging and stopping 모드들이 존재한다. 각각의 모드들을 모두 계산하여 각각의 최적 경로를 생성한 후, 최적 경로의 초기 jerk (부호도 포함하여)가 가장 작은 경로를 선택한다.

jerk(가속도의 변화량)가 ‘-‘ 이면 가속도가 줄어 들고 있는 상황 → 속도를 줄여하는 상황이므로 가장 작은 값을 선택

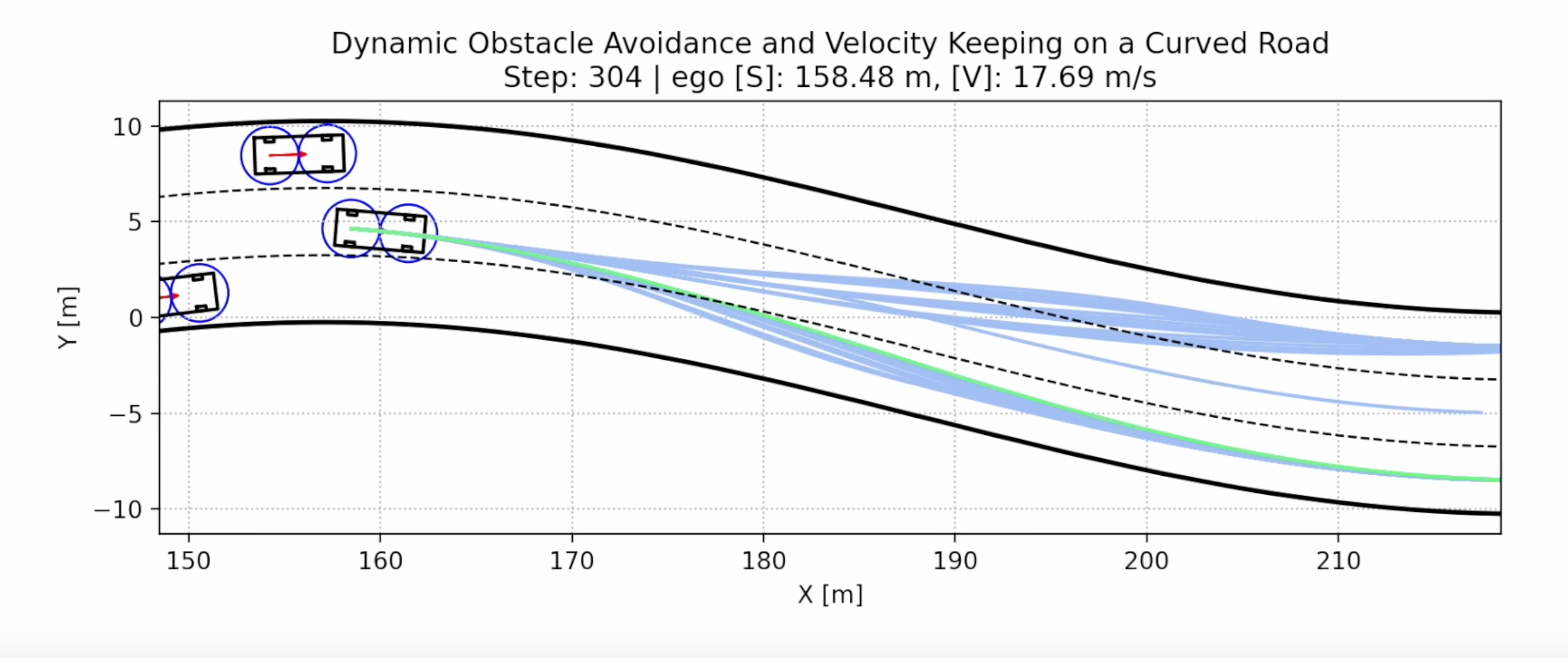
Result

해당 방식에 대한 3 가지 DEMO 영상을 보여준다.

1. 단순 정지
2. 정적 장애물 회피, 정지 (직선도로, 목표 속도: 20m/s, 위치: 400)
3. 동적 장애물 회피, 정지 (곡선도로, 목표 속도: 20m/s, 위치: 500)

코드 바로가기

시뮬레이션 결과 영상