Neural RRT*
Reference
Neural RRT*
Introduction
RRT*는 대표적인 sampling-based 알고리즘 중 하나로, 다양한 분야에서 활용되어 왔다.
이에 따라 많은 연구가 이 알고리즘의 효율을 개선하는 방법들을 제안했다.
대부분의 개선 기법은 RRT*의 샘플링 효율을 높이는 데 초점을 맞춘다.
즉, 기존의 uniform 샘플링 공간 대신 더 유망한 영역에서 샘플이 생성되도록 유도해 성능을 향상시킨다.
그중 Neural RRT*는 A* 와 Neural Network를 이용해 공간별 샘플링 확률을 예측하는 방식이다.
해당 방식에서는 A* 와 RRT*의 장점을 결합하여 사용한다.
- A*는 최단거리를 보장하는 알고리즘이다.
- 하지만 최단거리를 찾기 위해서는 많은 time cost와 memory cost 가 필요하다. 차원의 수가 커질 수록 cost들은 기하급수적으로 증가하게 된다.
- RRT*는 차원의 수가 높아도 빠르게 공간을 탐색한다.
- 하지만 최단거리를 보장하지 않는다. 점진적 최단거리로 수렴을 하지만 이를 위해서는 많은 time cost와 memory cost가 필요하다.
이에 따라 두 알고리즘의 단점을 보완하면서 장점을 어느정도 발휘할 수 있도록 설계되어져 있다.
간략한 모델 설명
CNN 모델인 Resnet50을 활용하여 A*의 결과로 나온 경로 이미지를 학습하여,
RRT*에서 사용할 픽셀별 확률 분포를 예측한다.
하지만 예측이 항상 연속적으로 나오지 않을 수 있기 때문에 0.5 확률로 Non-uniform(trained) / uniform sample을 사용하여 알고리즘을 수행하게 된다.
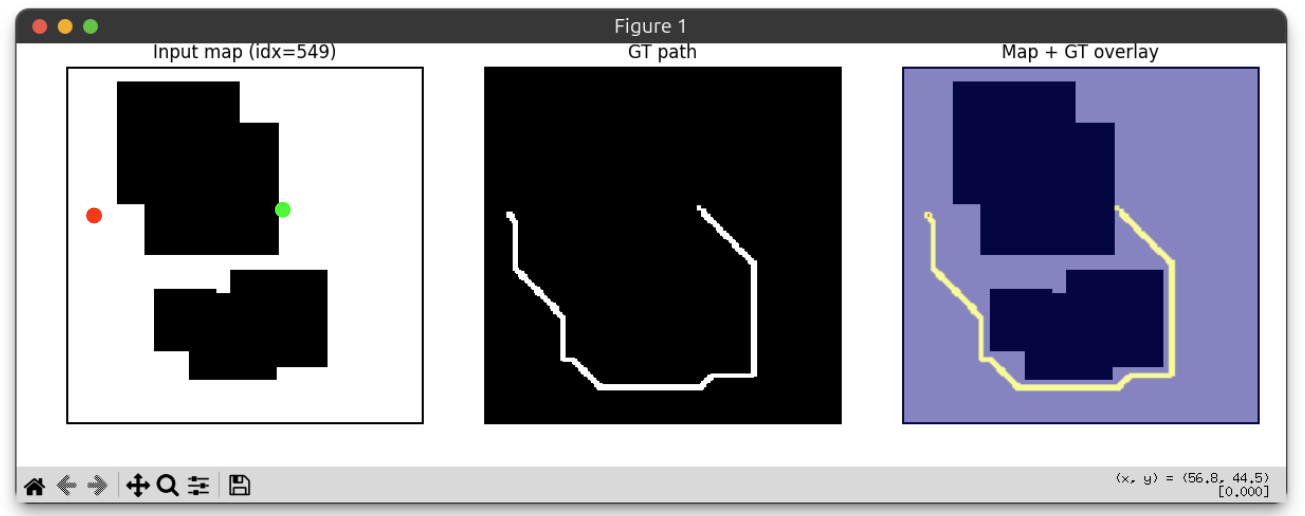
Dataset
| Data Encoding | Dataset Statistics | Data Split |
|---|---|---|
|
|
|
GT인 A* 경로의 두께를 학습의 안정성을 위해 1px -> 3px로 증강해서 사용한다. 경로가 너무 얇으면 픽셀 단위의 오차에 모델이 과도하게 민감해져 학습이 불안정해질 수 있으며, 신경망이 복잡한 지형 내에서 최적의 샘플링 영역을 일반화하여 학습하는 데 어려움이 있기 때문이다.
Restnet50의 계산 편의성을 위해 맵크기는 추후 pytorch의 Dataset으로 불러올때 224x224로 변환하여 사용하였다.
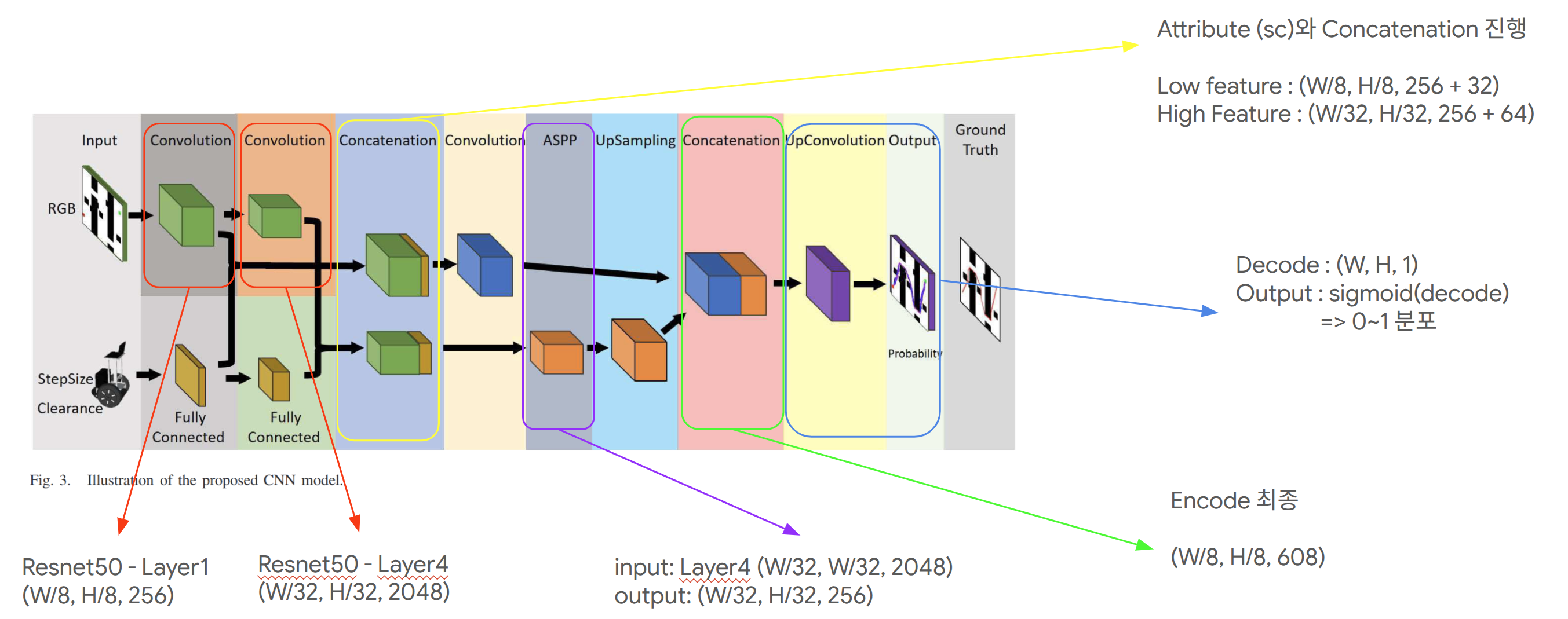
Model Architecture
해당 모델의 구조는 다음과 같다.
Input & Output
| Input | Output |
|—|—|
| Grayscale map image (free space / obstacle / start / goal 포함)
Robot attributes: Step size $S$, Clearance $C$
같은 map이라도 attribute에 따라 optimal path 분포가 달라지므로 이를 condition으로 함께 입력한다. | Probability map: $O \in [0,1]^{W \times H}$
각 pixel 값의 의미: $\hat p(u,v) = P(\text{optimal path passes through pixel})$ |
Map Encoder (Convolution: ResNet50)
환경의 공간 구조를 feature로 추출한다.
| Feature | 의미 | 해상도 |
|---|---|---|
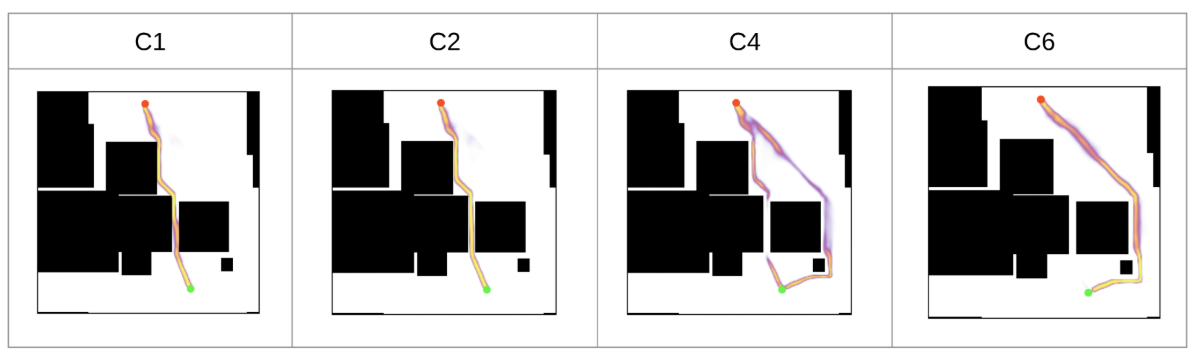
| C1 | low-level (local) | (W/8, H/8, 256) |
| C4 | high-level (semantic) | (W/32, H/32, 2048) |
- low-level → obstacle의 local structure
- high-level → map의 global topology
기존 Resnet50은 layer1의 shape이 (W/4, H/4, 256) 로 나와있어서,
resnet code에서 stride를 수정하여 논문과 shape을 동일게 맞췄다. (W/8, H/8, 256)
Attribute Encoder (FC)
| Encoder Input/Process | Output Feature |
|---|---|
| 입력 - step size - clearance 처리 - Fully connected layers - 두 단계 feature 생성 |
- $F_a^l$: $(1,1,32)$ - $F_a^h$: $(1,1,64)$ |
Feature Concatenation
Attribute feature는 spatial broadcast 후 map feature와 channel 방향으로 concat한다.
- Low branch: $C_1(W/8,H/8,256)$ + $F_a^l(1,1,32)$
$\rightarrow (W/8,H/8,256+32)$ - High branch: $C_4(W/32,H/32,2048)$ + $F_a^h(1,1,64)$
$\rightarrow (W/32,H/32,2048+64)$
이 과정을 통해 같은 map에서도 step size, clearance 조건에 따라 서로 다른 경로 확률 분포를 생성할 수 있다.
ASPP
High branch에는 ASPP(Atrous Spatial Pyramid Pooling)를 적용한다.
- 입력: $(W/32,H/32,2048+64)$
- 서로 다른 dilation rate의 atrous conv를 병렬 수행
- branch를 concat한 뒤 $1\times1$ conv로 channel 축소
- 출력: $(W/32,H/32,256)$
Upsampling (U-Net Decoder)
Decoder는 U-Net과 유사한 skip-connection 구조를 사용한다.
- ASPP 출력 $(W/32,H/32,256)$을 upsampling해 $(W/8,H/8,256)$으로 복원
- Low branch feature $(W/8,H/8,256+32)$와 concat
- Convolution block으로 융합하여 encoder 최종 feature를 구성
(구현 기준: $(W/8,H/8,608)$) - 추가 upsampling + conv로 $(W,H,1)$로 복원
- sigmoid를 적용해 최종 probability map을 출력
Train
학습 목표는 입력 map과 attribute가 주어졌을 때, 각 pixel이 optimal path에 포함될 확률을 예측하는 것이다.
출력은 sigmoid를 통과한 probability map이며, GT는 A* 결과를 기반으로 생성한 binary path mask를 사용한다.
Loss Function
논문 에서는 pixel-wise cross entropy를 사용한다.
\[\mathcal{L} = \sum \mathrm{CE}(O, G) + \lambda \,\mathrm{CE}(I, R)\]- $O$: network output probability map
- $G$: GT path label map
- $I$: input map
- $R$: map reconstruction head
- $\lambda$: 보조 항 가중치
논문을 보면 $R$에 대한 설명이 자세하게 나와 있지는 않지만, Recunstruction head를 모델에 추가하여 해당 vector를 가져왔다.
Inference to Planning
학습된 model은 추론 시 probability map을 생성한다.
NRRT*는 이 map을 non-uniform sampler의 prior로 사용하여, 유망한 영역에서 샘플링 비율을 높인다.
연속성이 끊길 수 있는 상황을 완화하기 위해 uniform sampling을 일부 혼합한다.
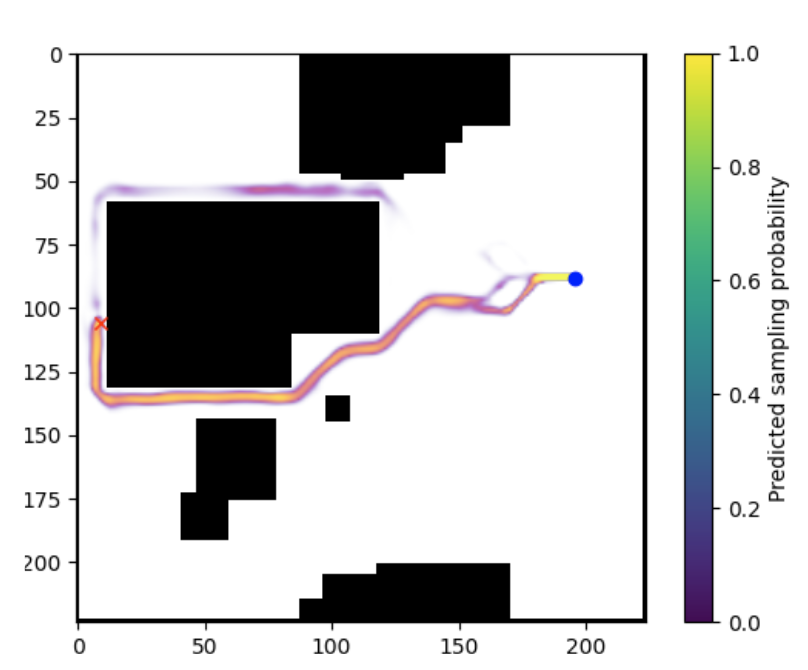
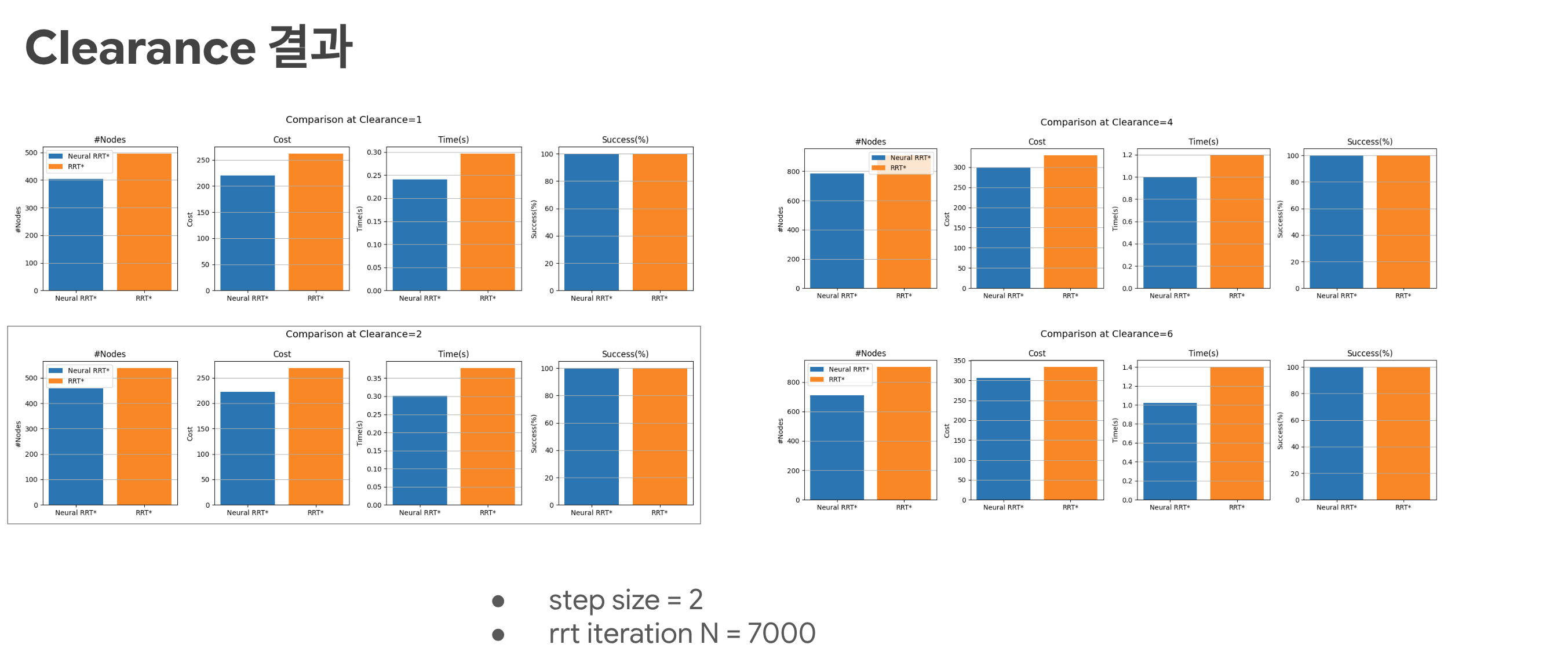
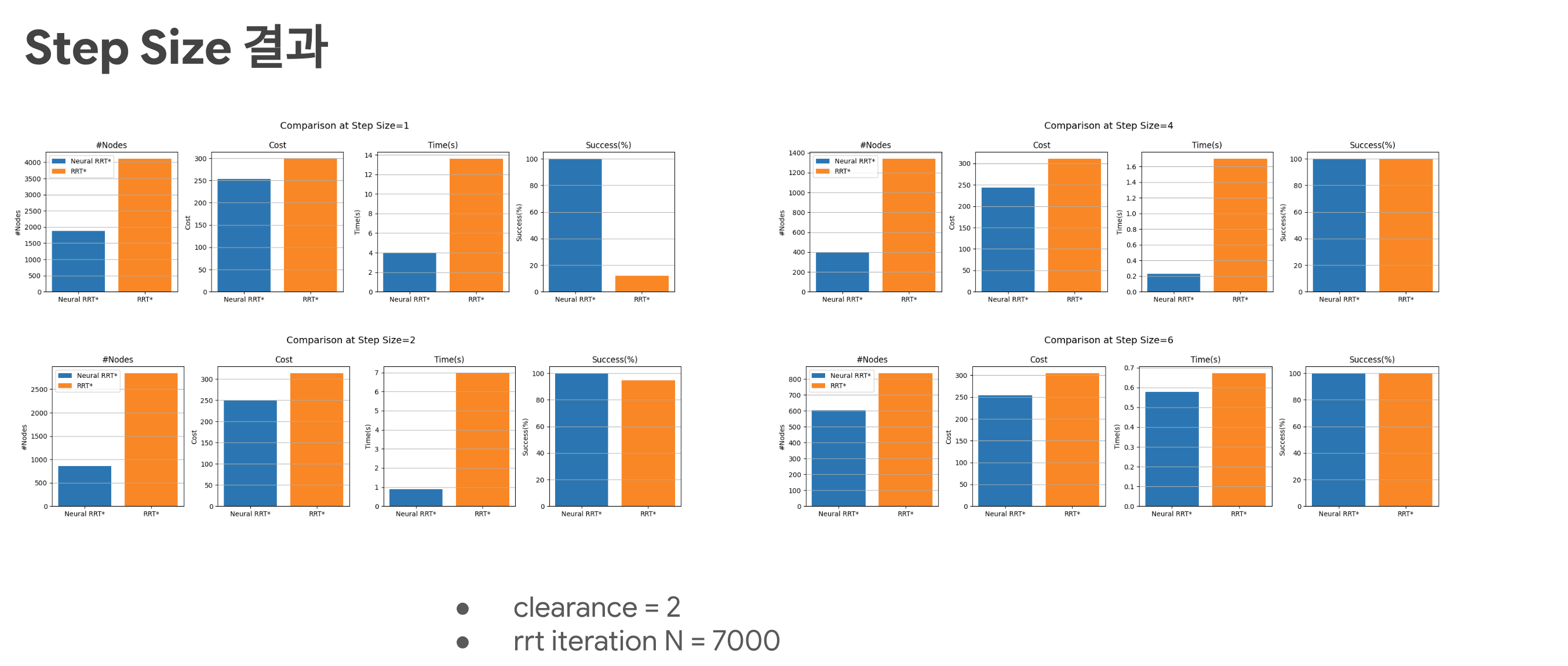
Result
아래 이미지는 NRRT* 기반 결과를 정리한 것이다.
| Result 1 (Clearance) | Result 2 |
|---|---|
 |
 |
| clearance 조건 비교 | RRT*와 시간 측정 비교 |
| Result 3 | Result |
|---|---|
 |
 |
| RRT*와 시간 측정 비교 | Step Size 6 Inferance |