Hybrid A* search algorithm
Reference
- Dolgov. D, Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments, IJRR, 2010
- https://medium.com/@junbs95/gentle-introduction-to-hybrid-a-star-9ce93c0d7869
Hybrid A* search algorithm
A*의 한계
A* 는 경로 탐색 문제에 많이 활용되고 있는 고전적인 알고리즘이다. 하지만 현실세계에 바로 적용하기에는 한계가 존재한다. 실제 자동차는 non-holonomic 제약을 가지고 있어, 자유롭게 모든 방향으로 움직이지 못한다. A*는 이런 제약을 고려하여 설계되지 않았기 때문에 실질적으로 적용하기 힘들다. 이를 해결하고 등장한 알고리즘이 Hybrid A* 알고리즘이다.
Hybird A* 소개
Hybrid A*는 기본적인 A*의 아이디어를 유지하면서, non-holonomic 제약을 만족하는 경로를 생성할 수 있도록 개선된 알고리즘이다. 이를 위해 kinematic bicycle model을 사용하여 차량의 실제 움직임을 모델링한다.
또한 기존 A*가 grid 기반의 discrete 탐색을 수행하는 반면, Hybrid A*는 A*의 discrete 탐색 노드에서 continuous 상태 정보를 이용해서 탐색을 수행한다. 이로 인해 실제 차량이 따라갈 수 있는 더욱 현실적인 경로를 생성할 수 있다.
kinematic model 이용한 expand
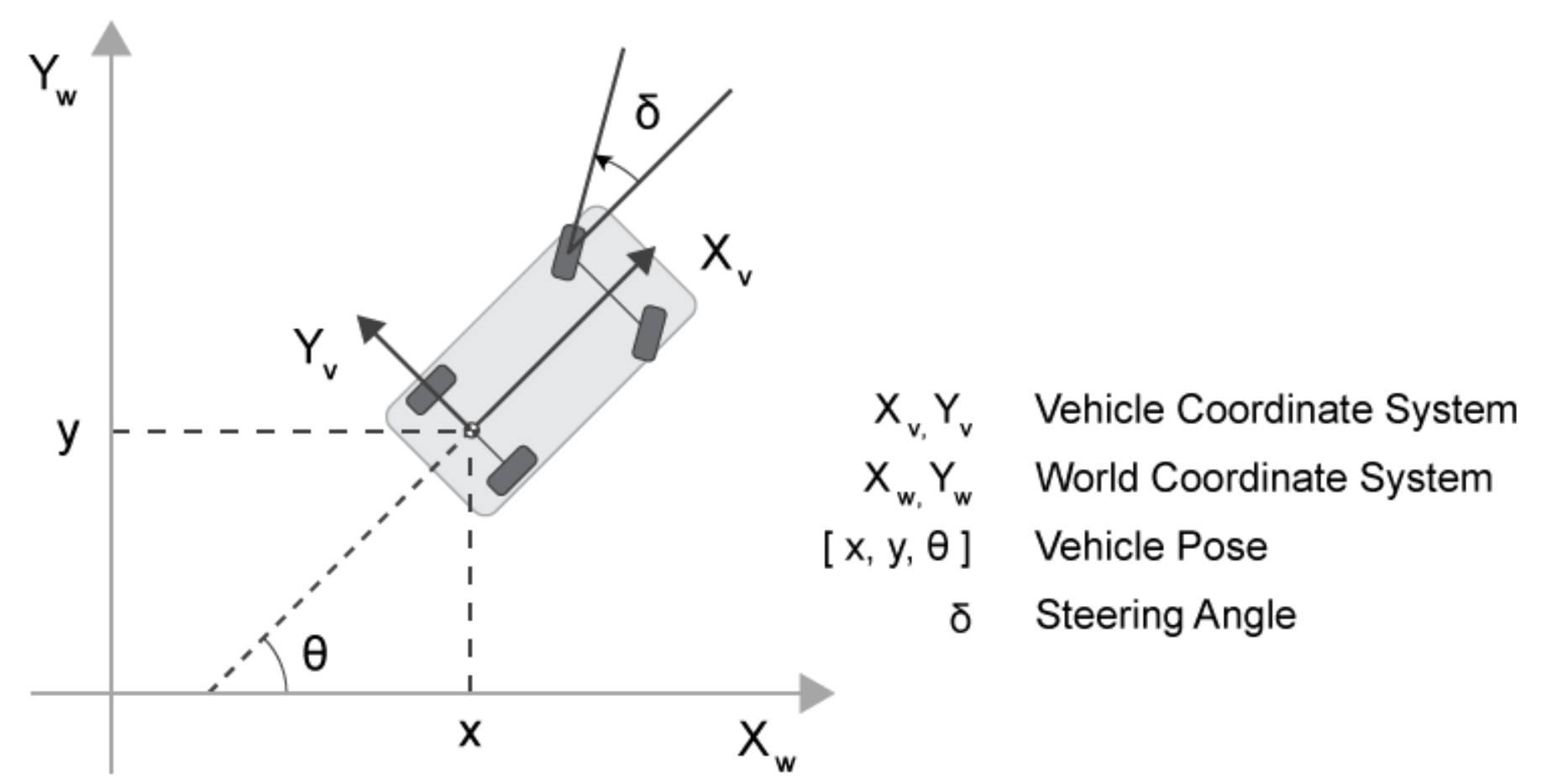
위의 kinematic 모델을 기반으로, Hybrid A*에서는 다음 노드를 확장할 때 실제 차량처럼 움직이도록 한다. 내 구현에서는 steering angle을 조절하여 action set을 구성하고, 이를 통해 연속적인 상태 공간에서 다음 상태를 계산한다. 이때의 새로운 노드는 이후 discrete한 grid cell 정보와 현재 연속적인 상태를 함께 저장하여 다음 상태를 위해 사용한다.
또한, 후진 동작에는 곱셈 페널티를, 전진과 후진이 전환될 때에는 덧셈 페널티를 적용하였다. 이를 통해 실제 차량 운전과 유사한 경로 선택을 유도한다.
동일한 grid cell에 도달하더라도 여러 상태(예: yaw, steering angle 등)가 존재할 수 있다. 이 경우, Hybrid A*는 가장 비용이 낮은 상태만 유지하고, 나머지 분기는 모두 제거하여 탐색 공간을 관리한다.
이렇게 찾아가는 경로는 운전가능을 보장하지만, 최소 비용을 가는 경로를 찾는 것은 보장되지는 않는다.
추가로, 경로 생성을 위해 Dubins 곡선이나 Reed-Shepp 곡선을 사용할 수도 있다. 이러한 기법들은 더 자연스러운 경로 생성이 가능하고, 거리 기반 비용 계산에서도 보다 정확한 평가가 가능하다고 생각한다. (비교해볼 예정, 현재 공부중)
두 가지 heurstic
확장을 위한 비용 추정 계산(cost-to-goal)에 사용되는 heuristic은 두 가지가 존재한다.
non-holonomic-without-obstacles
이 heuristic은 자동차와 같이 non-holonomic 제약이 적용된 상태에서, 장애물을 무시하고 목표 지점까지의 가장 짧은 거리 비용을 추정한다. 4차원 공간 (x, y, yaw, r) 상의 모든 점에서 목표 지점까지 도달하는 경로를 평가하며, 일반적으로 Reed-Shepp path를 기반으로 한다.
이 heuristic은 센서로 인식되는 정보가 필요없기 때문에 사전에 미리 계산하여 사용할 수 있다.
내 구현에서는 Reed-Shepp 곡선을 사용하지 않고, steering angle을 조정하는 방식으로 여러 가능한 움직임을 시뮬레이션하여 그 중 가장 적절한 cost를 계산하는 방식으로 구현하였다. 이 과정에서 후진, 방향 전환, heading 차이 등에 따라 가중 cost를 부여하여 실제 차량 움직임과 유사한 비용 모델을 구성하였다.
이 heuristic은 목표 지점에 도달할 때의 방향(heading) 을 고려하므로, 잘못된 방향으로 진입하는 경우에는 더 높은 cost를 부과한다. 이를 통해 목표 지점에 올바른 방향으로 도달하도록 유도할 수 있다.
holonomic-with-obstacles
이 heuristic은 non-holonomic 제약을 무시한 채, A*처럼 discrete하게 움직이며 장애물을 고려하여 현재 위치에서 목표 지점까지의 가장 짧은 거리를 추정한다. 2차원 공간 (x,y) 상에서 DP 를 사용하여 grid map 기반의 비용 계산한다.
이 두 heuristic 값 중에 더 큰 값을 해당 grid에서의 heuristic으로 최종 선택하여 사용하게 된다.
Analytic Expansions
위의 설명은 보면 이산화된 control actions의 상태 들이다. 이는 연속적인 공간의 목표점에 도달하지 못할 수도 있다는 이슈가 생길 수 있다. 또한 모든 acions를 확인하기 때문에 탐색 속도가 저하될 수 있다. 이를 위해 analytic expansions 를 이용해 개선 할 수 있다.
reed-shepp path를 이용해 목표점 까지의 최적 경로를 계산하고 이 경로상에 장애물이 없다면 해당 경로를 자식 노드로 추가시키는 방식이다.
(아직 나는 구현해보지 못했다..)
현재 내 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
def planning(self):
# setting start node and goal node
start_node
goal_node
# penalty constants
move_cost = 1
reverse_move_cost = 10
change_direction_cost = 50
steering_cost = 1
diff_yaw_cost = 2
# calculated two heurstic tables
non_holonomic_table = non_holonomic_without_obstacles()
holonomic_table = holonomic_with_obstacles()
open_set, closed_set = {}, {}
open_set[map.get_grid3D_idx(start_node)] = start_node
while open_set:
curr_id = min(open_set, key=lambda o:open_set[o].f)
curr = open_set[curr_id]
del open_set[curr_id]
closed_set[curr_id] = curr
if is_goal(curr, goal_node):
goal_node.p_idx = curr_id
break
for steer, direction in bicycle_action_command():
rx, ry, ryaw = vehicle.action(curr_continuos_state, steer, direction)
nx, ny = calc_grid_xy(rx, ry)
nyaw = calc_grid_yaw(ryaw)
# check is not map point
if not map.verify_node(nx, ny):
continue
if vehicle.is_collision(map, curr_continuos_state):
continue
# calculating g cost (including change direction, sterring angle etc..)
next_g_cost = move_cost
next_g_cost *= (direction == -1) * reverse_move_cost + (direction == 1) * 1
next_g_cost += (direction != curr.r) * change_direction_cost
next_g_cost += abs(np.rad2deg(steer)) * steering_cost
next_g_cost += abs(curr.yaw - nyaw) * diff_yaw_cost
next_g_cost += curr.g
next_node = Node(nx, ny, nyaw, rx, ry, ryaw, direction, next_g_cost, p_idx=curr_id)
h_idx = map.get_grid2D_idx(next_node)
nh_idx = map.get_grid3D_idx(next_node)
if nh_idx in closed_set:
continue
if h_idx not inholonomic_table:
holonomic_table[h_idx] = 0.0
if nh_idx not in non_holonomic_table:
non_holonomic_table[nh_idx] = 0.0
next_node.h = max(holonomic_table[h_idx], non_holonomic_table[nh_idx])
next_node.f = next_g_cost + next_node.h
if nh_idx not in open_set or open_set[nh_idx].f > next_node.f:
open_set[nh_idx] = next_node
return get_final_path(closed_set, goal_node)