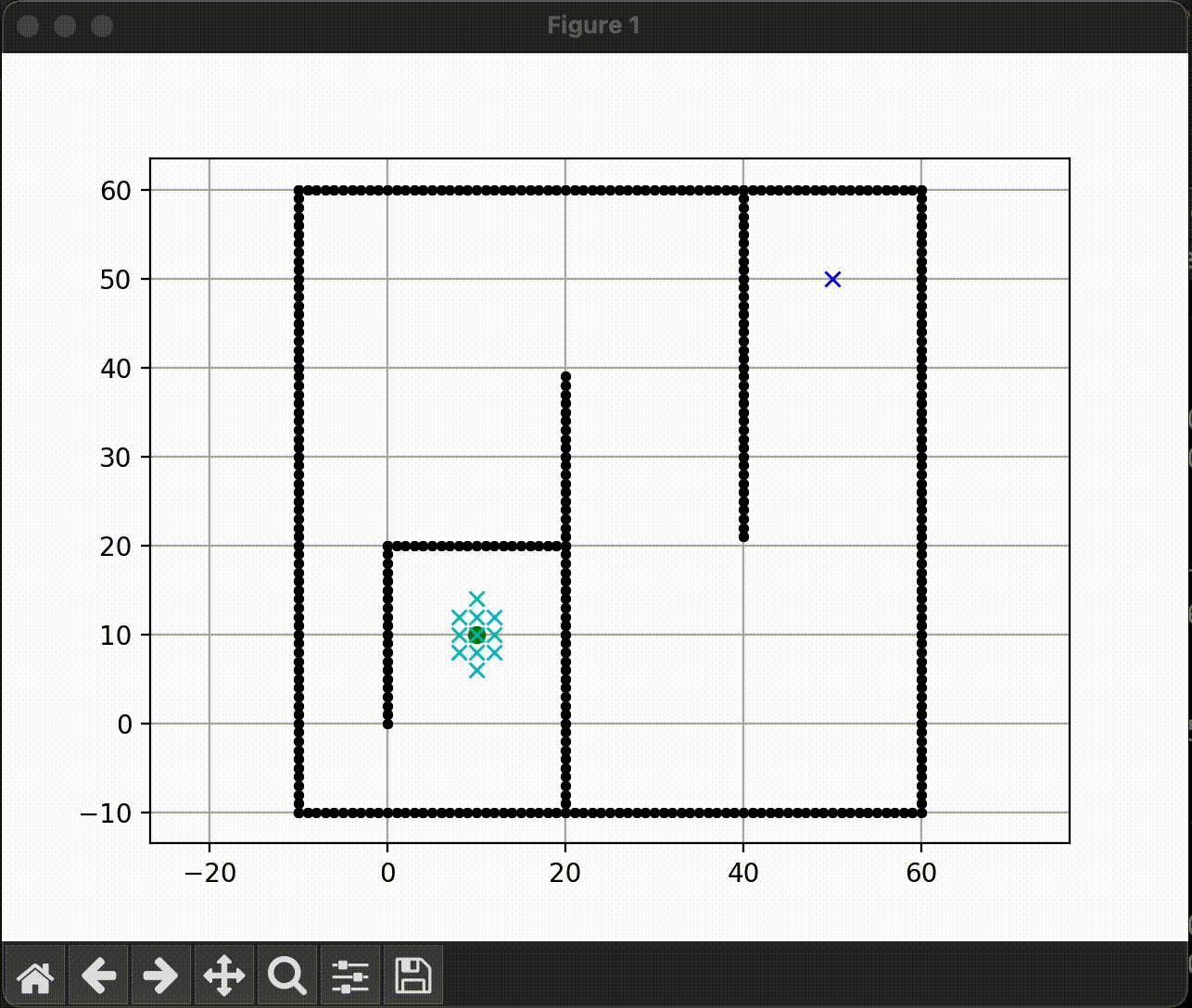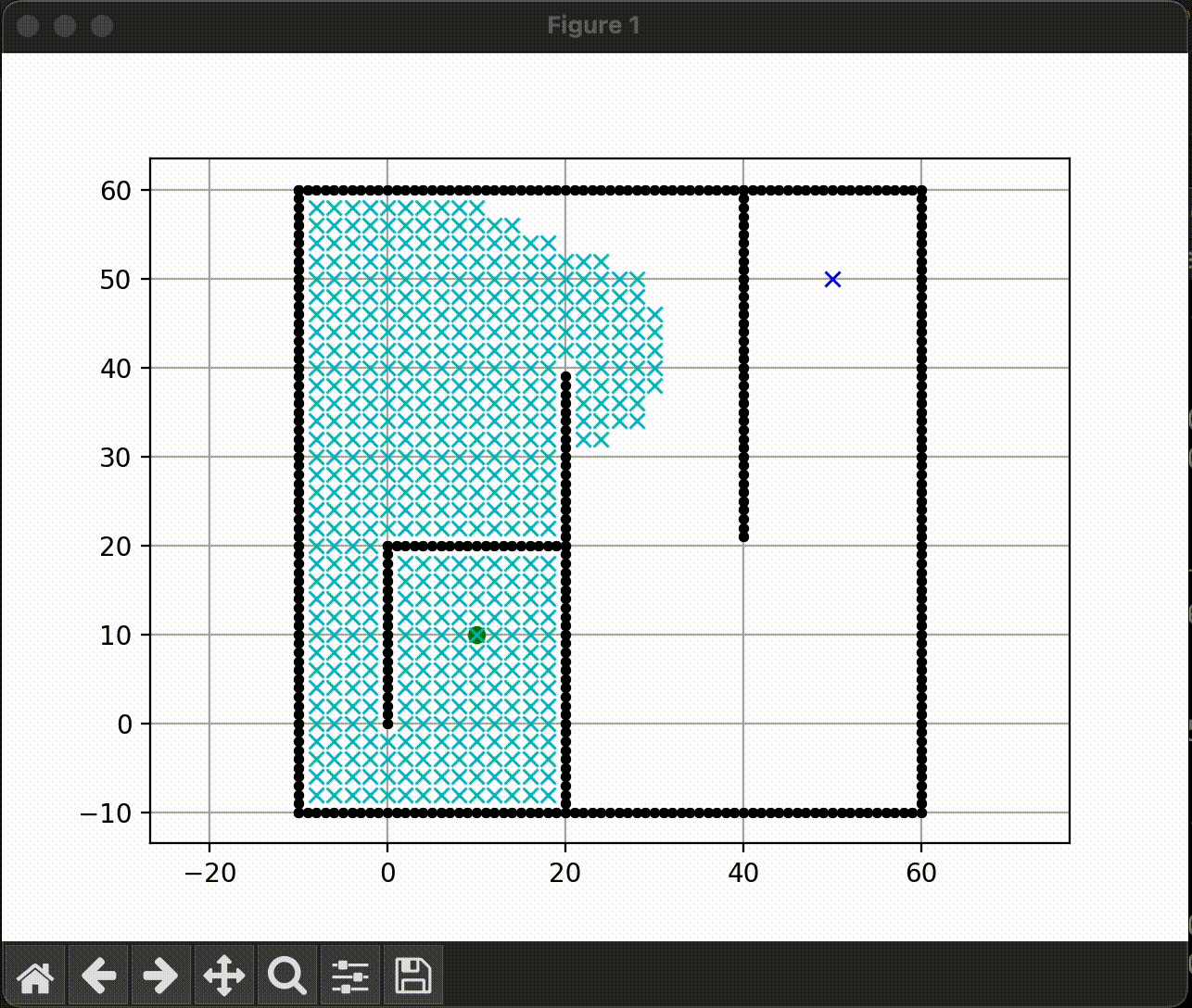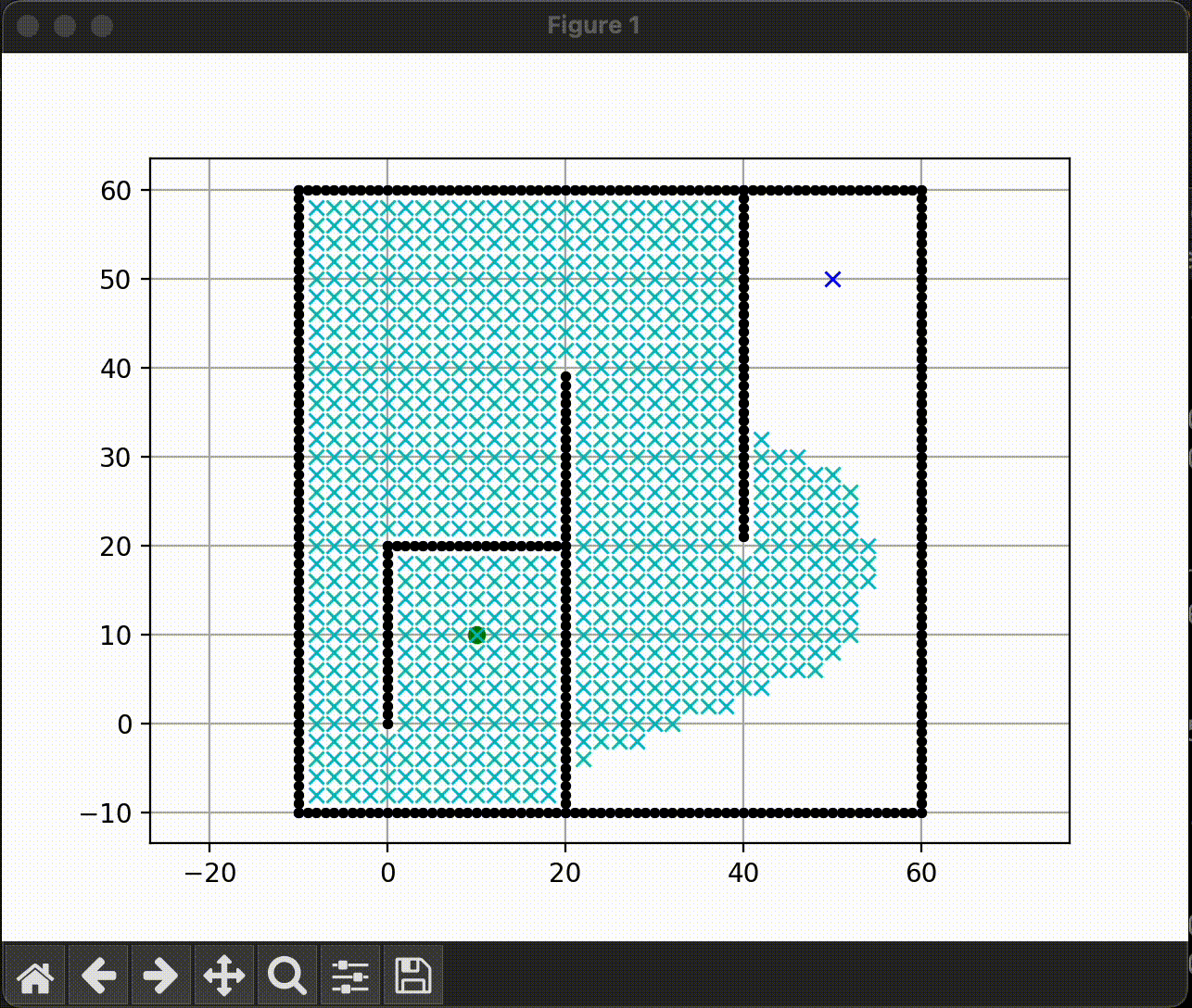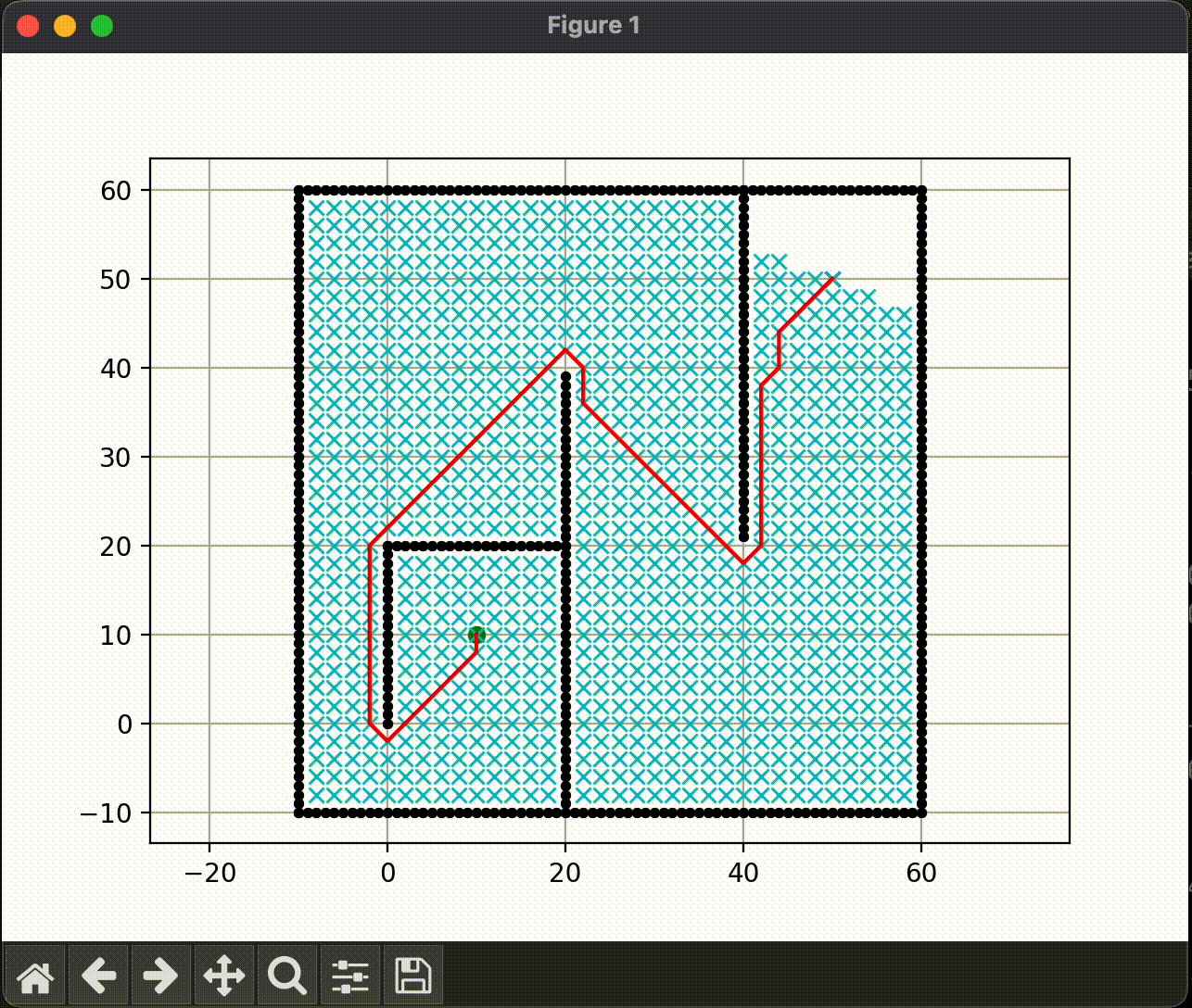
A* search algorithm
참고한 글
- https://theory.stanford.edu/~amitp/GameProgramming
- https://atsushisakai.github.io/PythonRobotics/modules/5_path_planning/grid_base_search/grid_base_search.html#a-algorithm
A* search algorithm
A* 소개
A*는 2d grid 공간에서 효율적인 길찾기 알고리즘이다. 즉, 최대한 빠르고 짧은 거리를 찾지위해 고안된 알고리즘이다. 이를 위해 Dijkstra의 장점과 GBFS (Greedy Best First Search)의 장점을 이용해 다양한 여러 상황에도 최대한 효율적인 길찾기가 가능하다.
그래서 현대의 네비게이션들이 A*를 기반으로 응용된 알고리즘을 사용하고 있다.
Dijkstra & GBFS 간략한 설명
Dijkstra
Dijkstra는 유명한 경로 탐색 알고리즘이다. 해당 알고리즘은 시작지점과 가까운 점부터 탐색을 시작하여 목표지점까지의 경로를 모두 탐색한다. 따라서 최단 거리를 반드시 보장한다.
하지만 목표지점까지 가기전 시작지점과 더 가까운 점들을 모두 탐색해야한다는 단점이 존재한다. 빠른 탐색을 할 수 없다.
Dijkstra
간단한 경로지만 탐색 범위가 넓음 |
Greedy-BFS
빠르게 목표에 도달 |
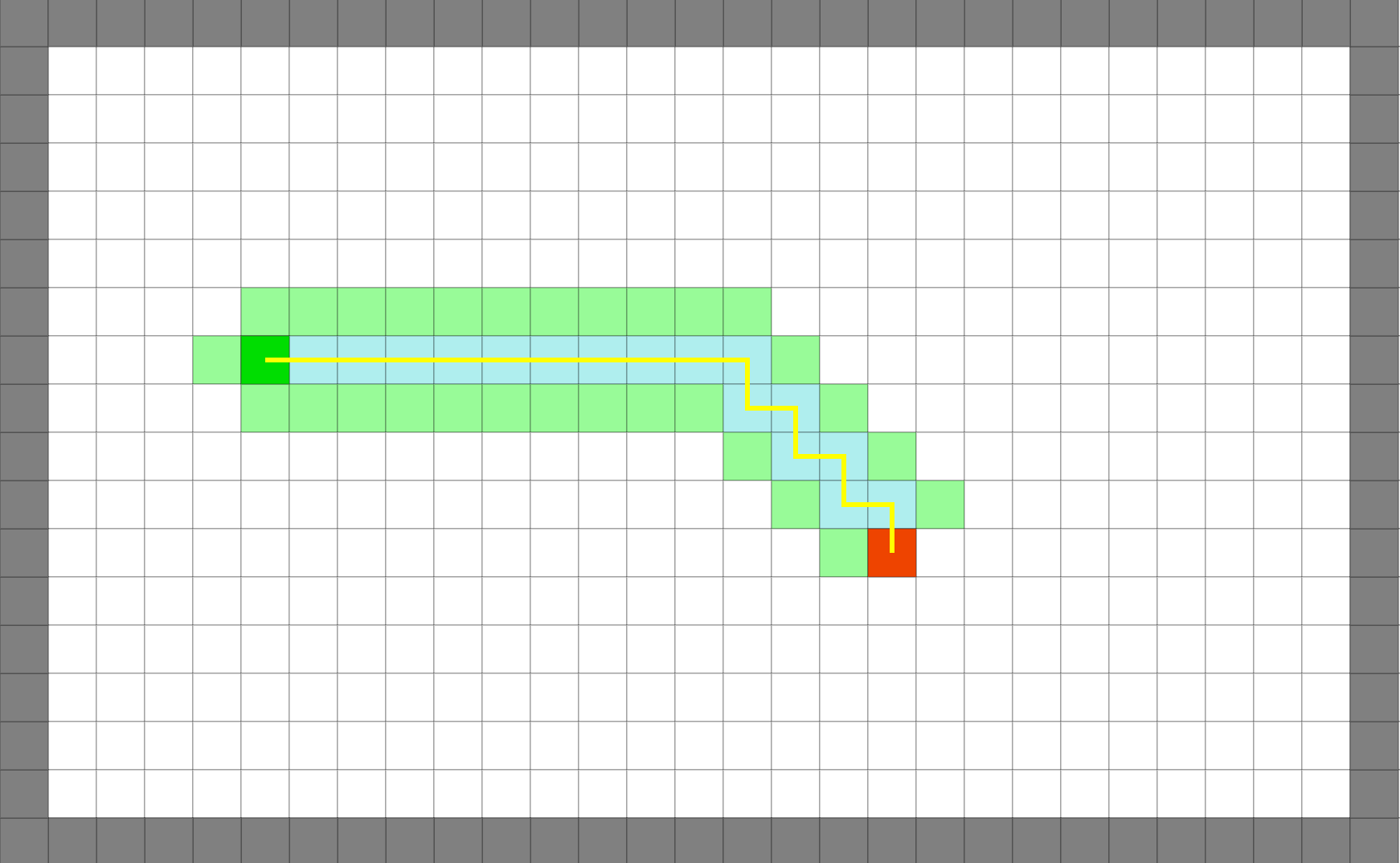
GBFS (Greedy Best First Search)
GBFS는 실제 거리는 알기 힘들기 때문에 huristic 함수을 이용해서 목표지점까지의 경로를 찾는 방식이다. 비용이 가장 적은 방향으로 길을 찾아 나간다.
💡 huristic 함수은 현재지점에서 목표지점까지의 비용을 추정하는 함수라고 생각하면된다.
⚙️ huristic의 대표적인 종류
- Manhattan
- Eucliden
대체로 Dijkstra보다 좋은 성능을 보여주지만 모든 상황에서 그러지 못한다. 아래와 같이 커브가 있는 상황에서는 Dijkstra가 더 효율적인 경로를, GBFS는 비효율적인 경로를 선택할 수 있다. 즉, 항상 최단거리를 보장하지 않는다.
Dijkstra
최적의 경로를 찾지만 탐색 범위가 넓음 |
Greedy-BFS
빠르게 목표에 도달하지만 최적이 아닐 수 있음 |
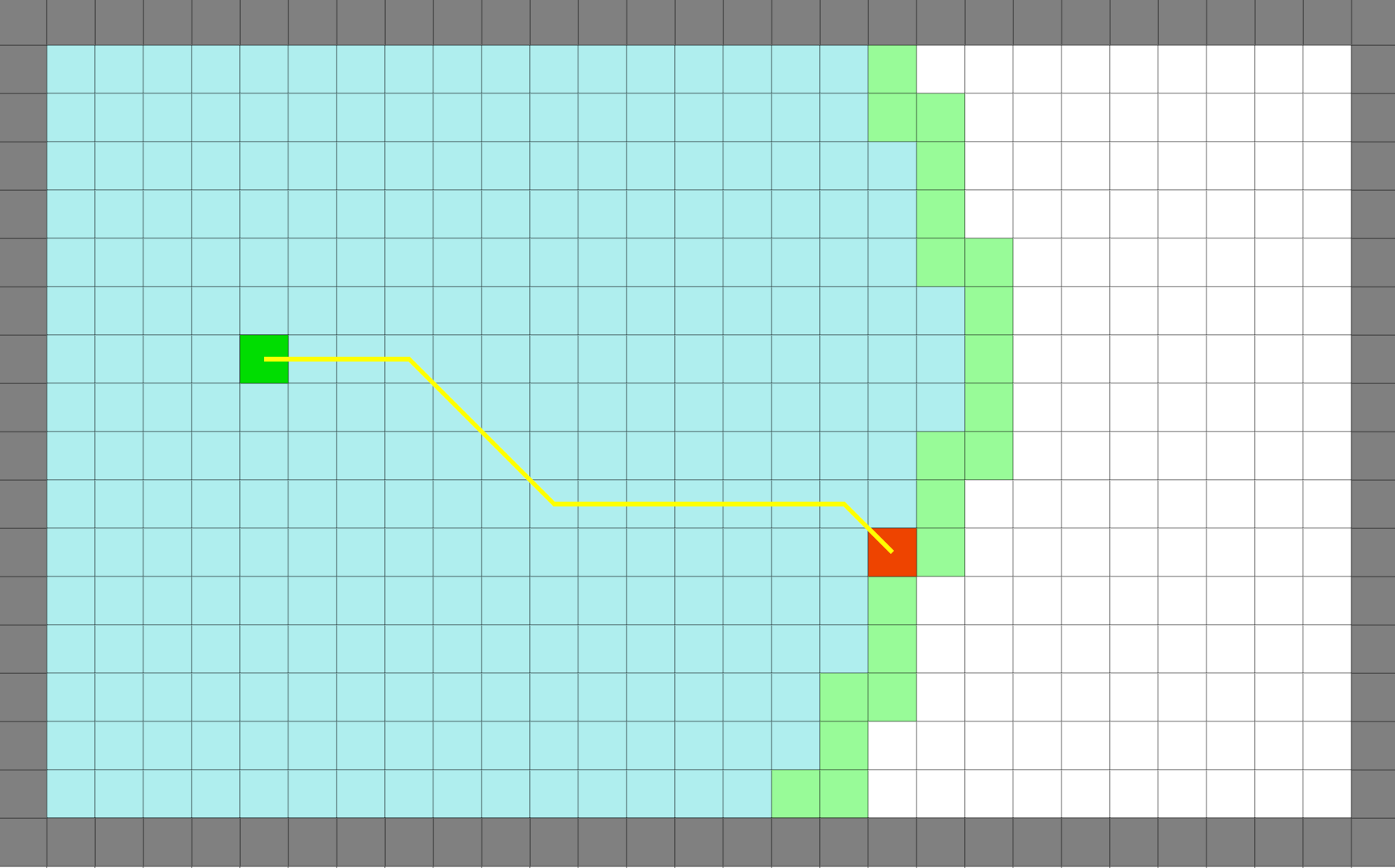
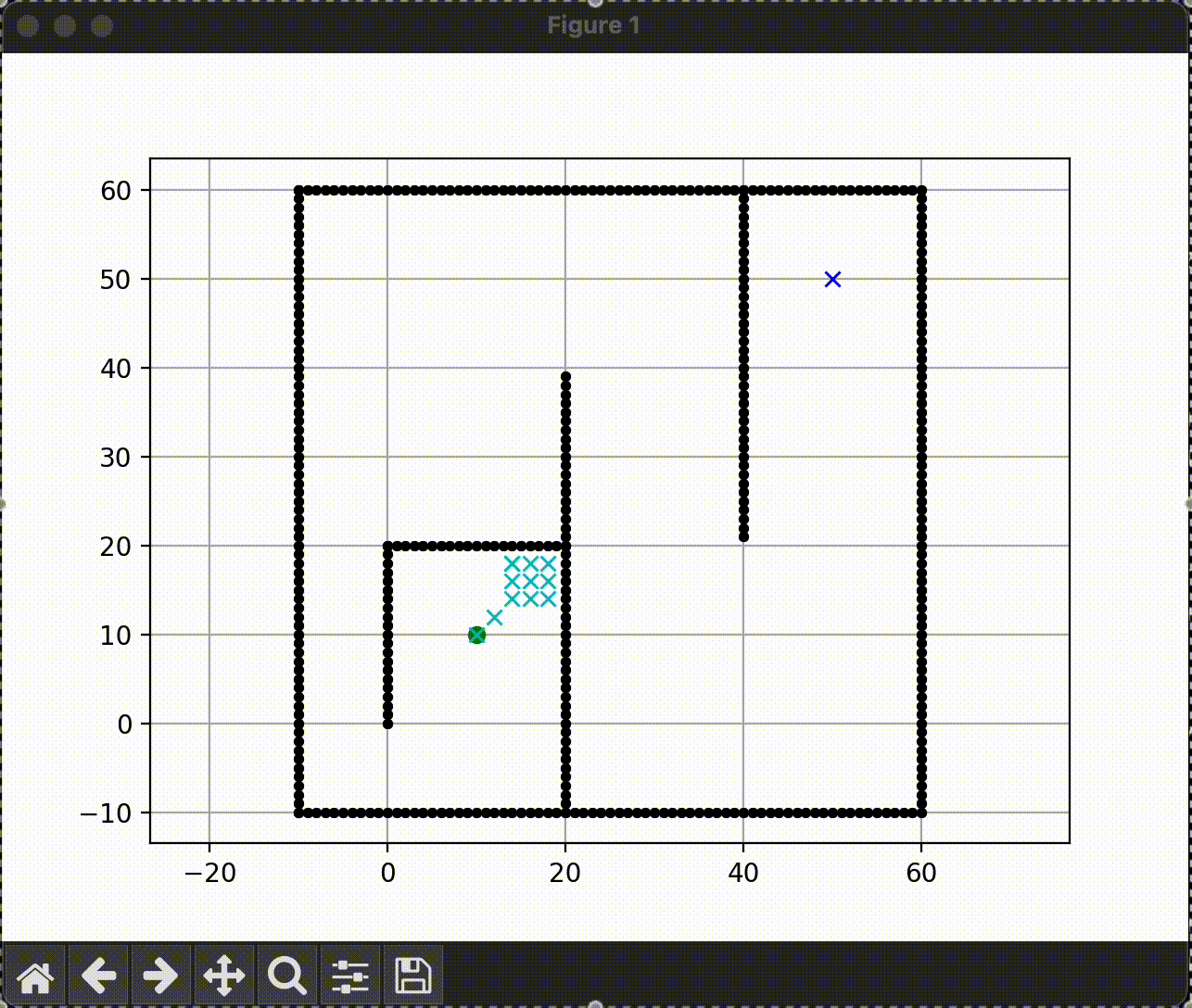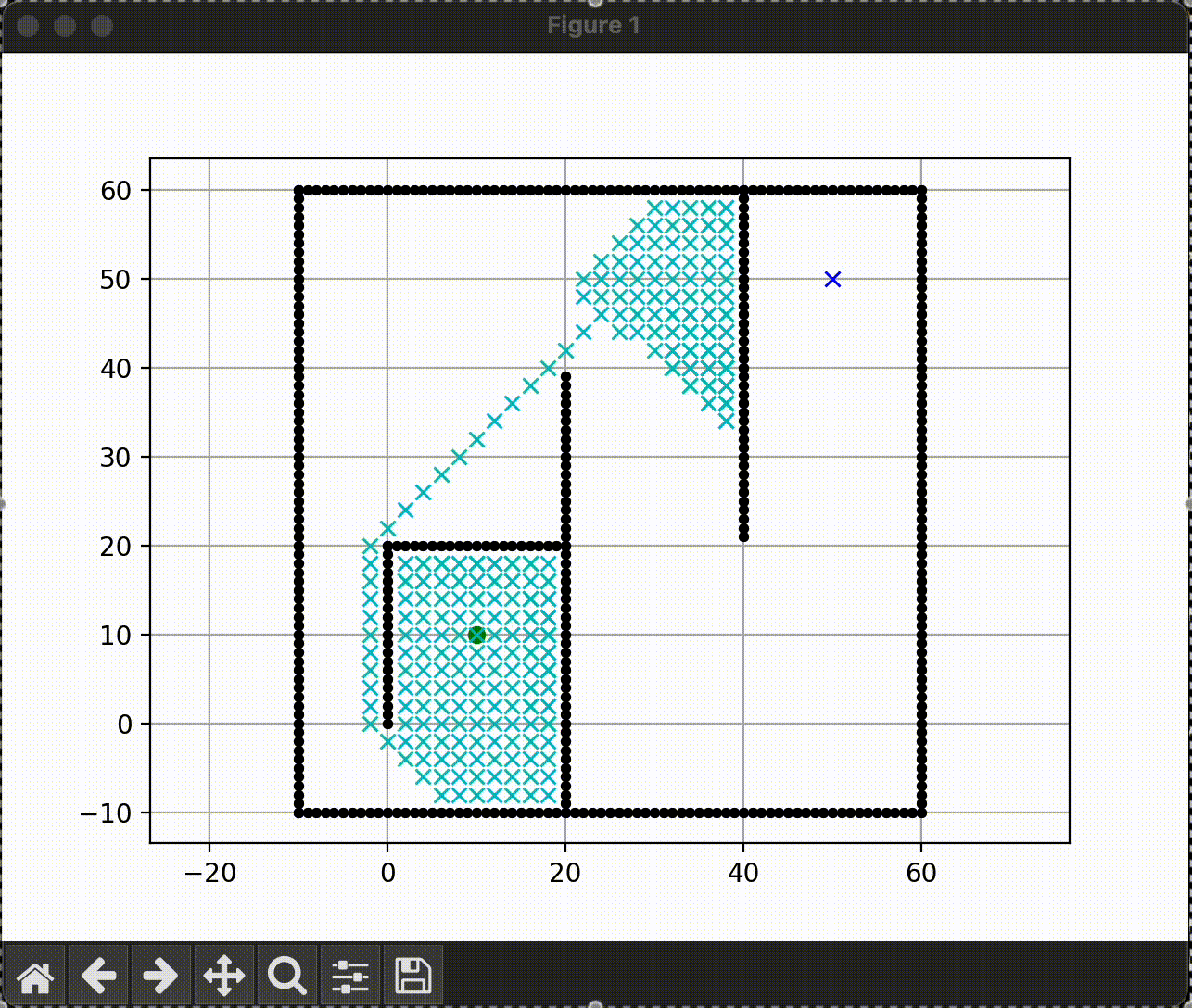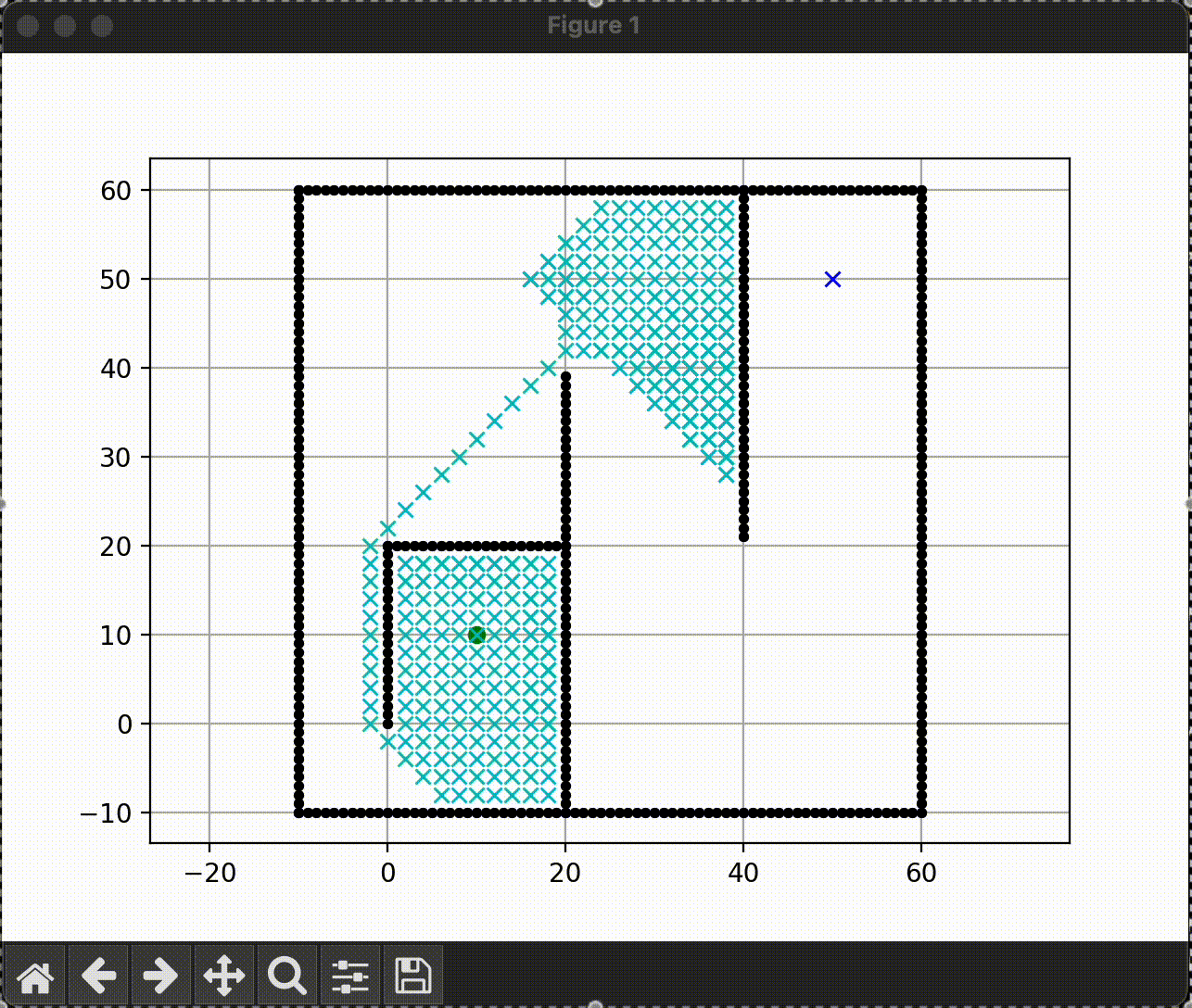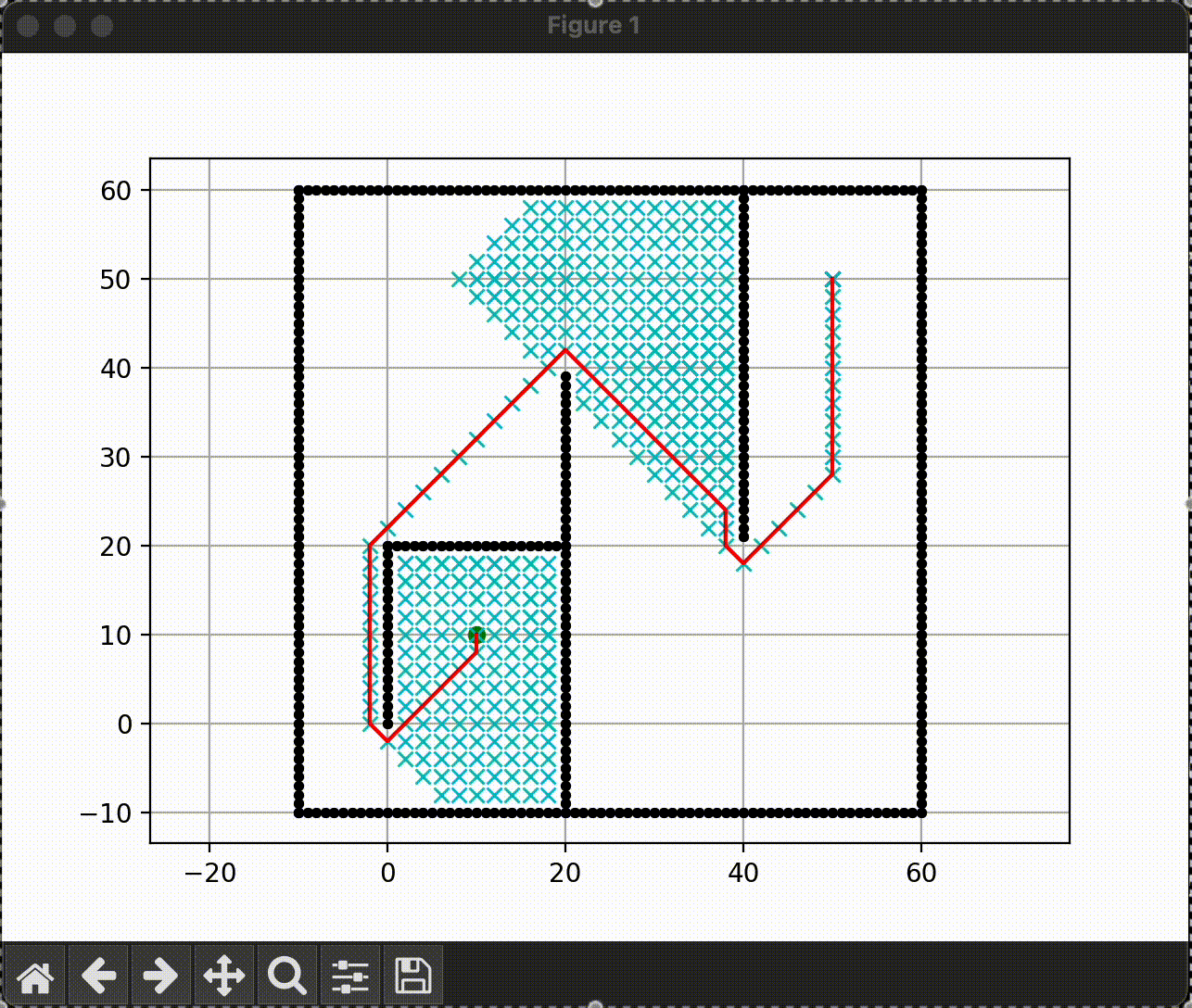
A* Search
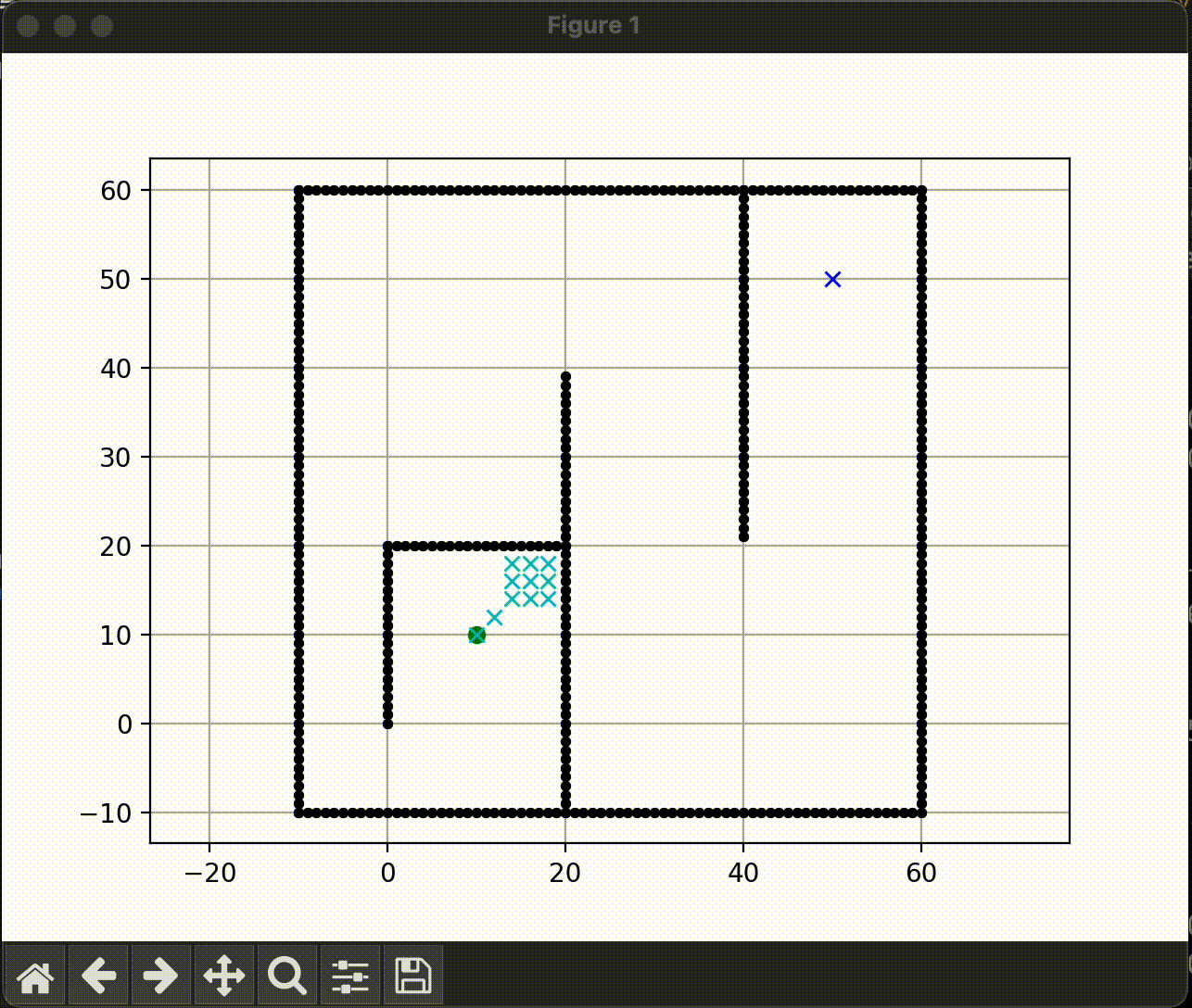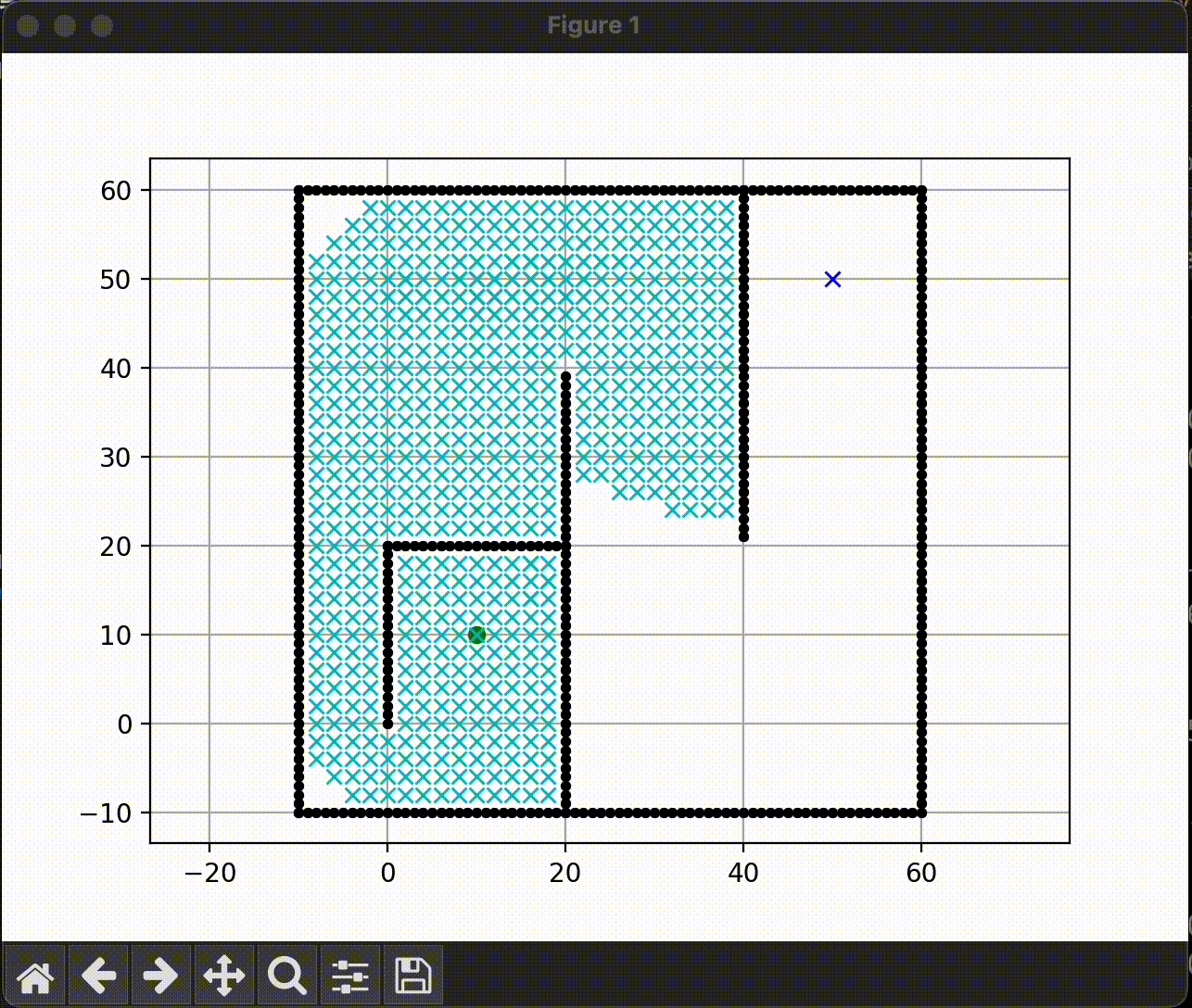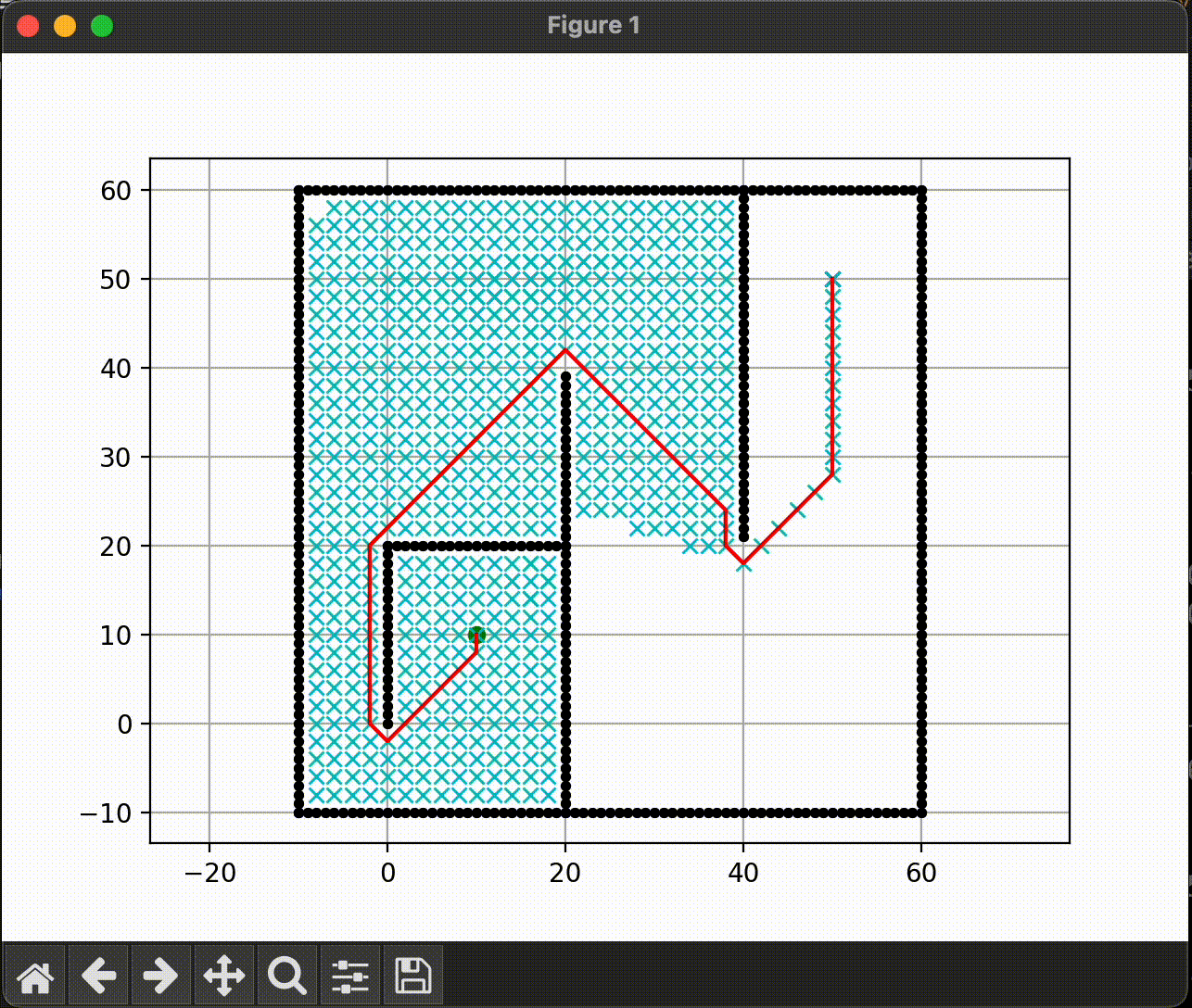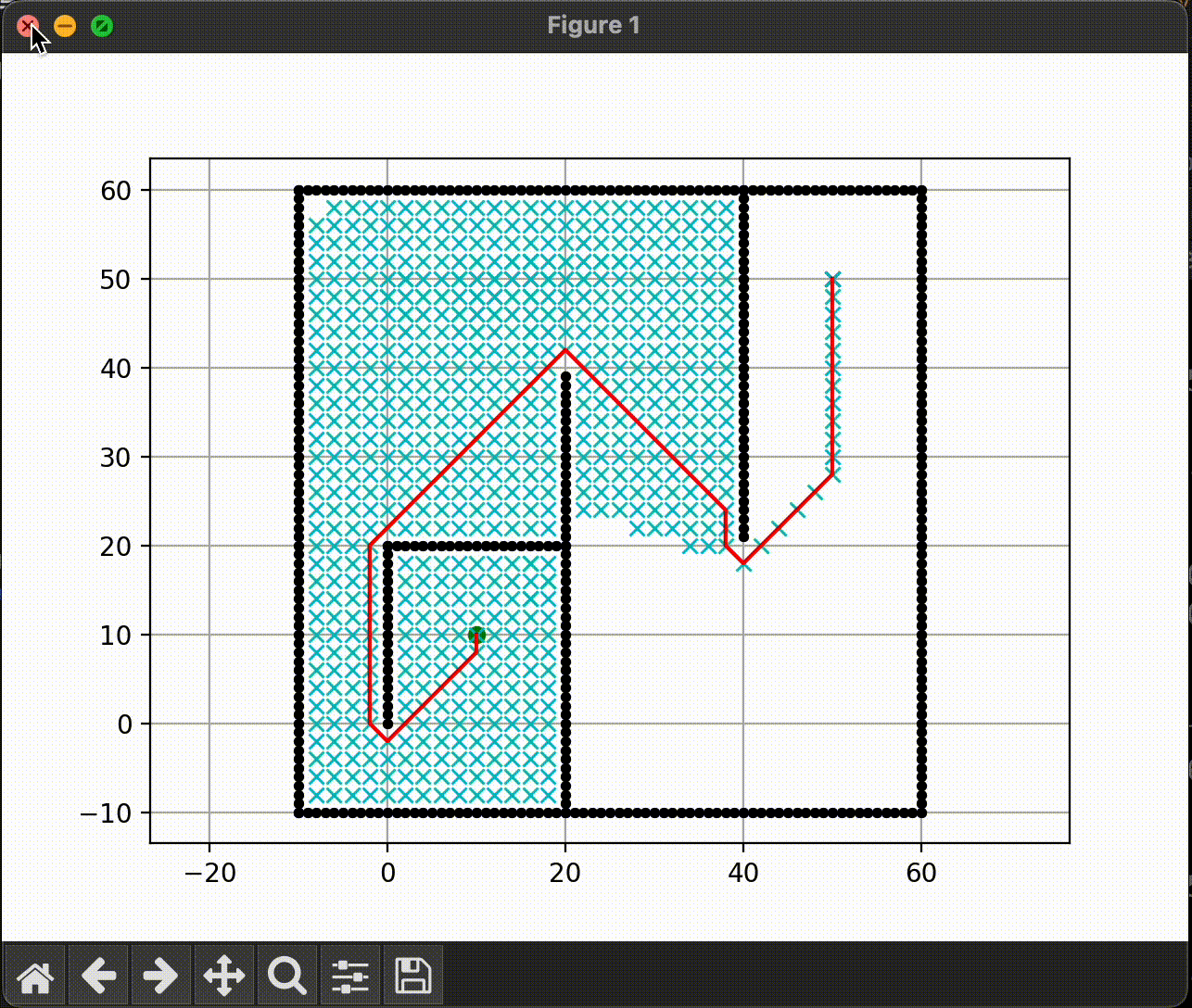
따라서 최대한 최단거리도 보장하면서 빠른 탐색을 위해 등장한 알고리즘이 A star이다.
A* 는 dijkstra의 시작 지점으로 부터의 cost 추정 g(n) 과 greedy-bfs의 huristic을 이용한 비용 추정 h(n) 을 모두 사용하여 비용을 계산하고 이를 이용하여 경로를 탐색한다. f(n) = g(n) + h(n) 을 이용한다.
즉, f(n)의 값이 작은 방향으로 경로를 찾게 된다.
huristic의 영향
- h(n) == 0 → dijkstra 사용, 최단거리 보장, 느림
- h(n) <= (실제 목표까지의 비용)
→ A*는 최단 경로를 보장, but h(n)이 작을 수록 탐색범위가 확장되어 속도가 느려짐 - h(n) == (실제 목표까지의 비용)
→ 이상적인 경우, 정확하고 빠르게 동작 - h(n) > (실제 목표까지의 비용)
→ 최단경로는 보장하지 않아도, 빠르게 동작함
위의 상태들을 이용해서 h(n)의 값을 조절하여 속도와 정확성중에 하나를 선택할 수 있다.
f(n) = g(n) + w * h(n)
| 가중치 (w) | 알고리즘 성격 | 속도 | 최적 경로 |
|---|---|---|---|
| w > 1 | Greedy (공격적) | 빠름 | 보장 안됨 |
| w = 1 | A* (균형적) | 보통 | 보장됨 |
| 0 ≤ w < 1 | Dijkstra-like (보수적) | 느림 | 보장됨 |
| w = 0 | Dijkstra (맹목적) | 매우 느림 | 보장됨 |
구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
open_set = dict()
closed_set = dict()
open_set[calc_grid_index(start_node)] = start_node
while len(open_set):
curr_id = min(open_set, key=lambda o: open_set[o].g + open_set[o].h)
curr = open_set[curr_id]
del open_set[curr_id]
closed_set[curr_id] = curr
if curr.x == goal_node.x and curr.y == goal_node.y:
goal_node.p_idx = curr_id
break
for motion in motions:
mx, my, cost = motion
neighbor_node = Node(curr.x + mx,
curr.y + my,
curr.g + cost,
heuristic(goal_node, curr.x + mx, curr.y + my),
curr_id)
neighbor_id = calc_grid_index(neighbor_node)
if not grid_map.verify_node(neighbor_node):
continue
if neighbor_id in closed_set and closed_set[neighbor_id].g > neighbor_node.g:
del closed_set[neighbor_id]
if neighbor_id in open_set and open_set[neighbor_id].g > neighbor_node.g:
del open_set[neighbor_id]
if neighbor_id not in open_set and neighbor_id not in closed_set:
open_set[neighbor_id] = neighbor_node
각 탐색 알고리즘 비교
Dijkstra
|
Greedy-BFS
|
A* search
|
A* 기반 알고리즘
많은 다양한 알고리즘이 존재한다.
-
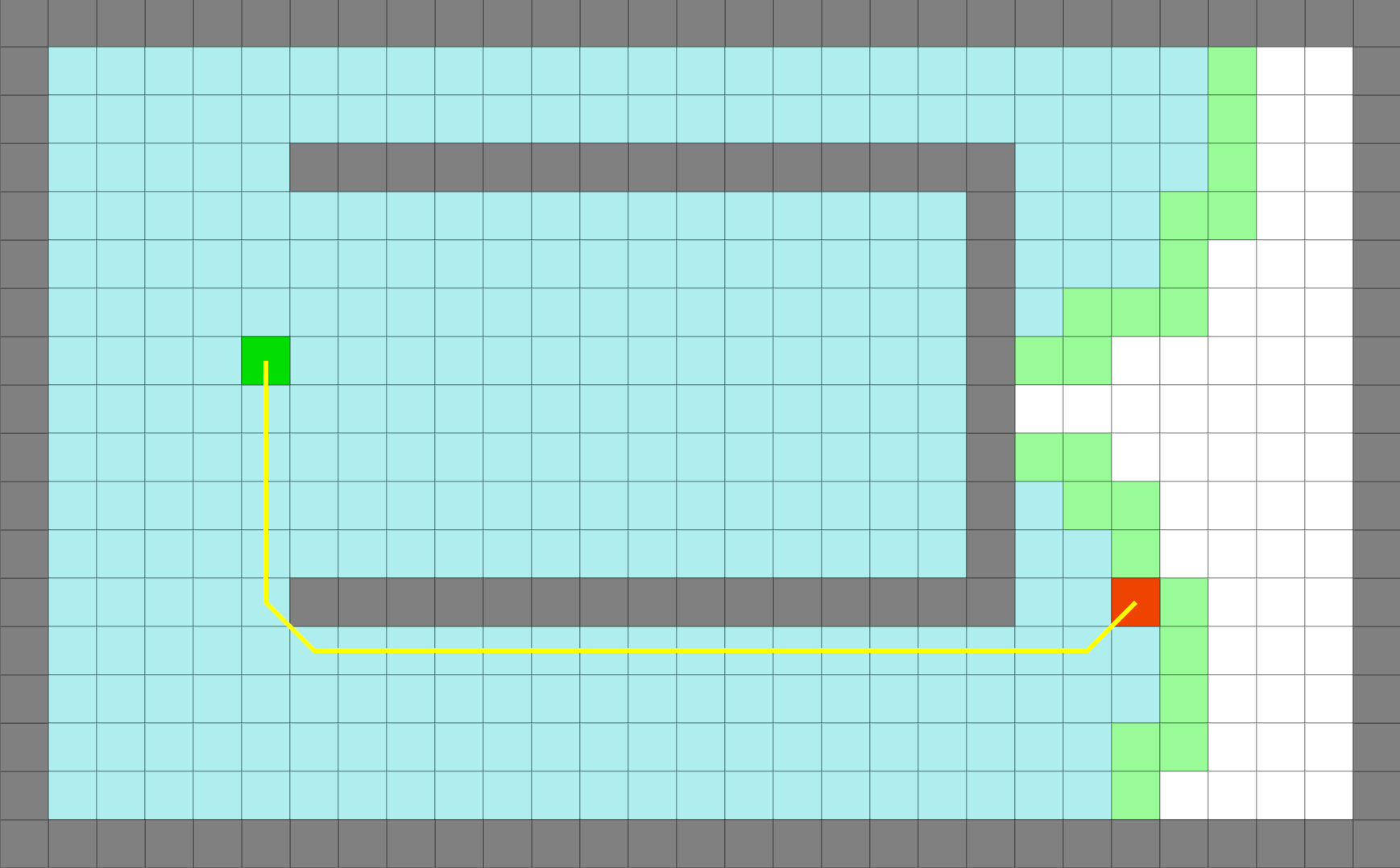
Bidirectional A*
→ (출방 -> 목적지), (목적지 -> 출발) 양방향으로 A*을 수행한다.
→ 서로가 만나면 알고리즘을 중단한다. -
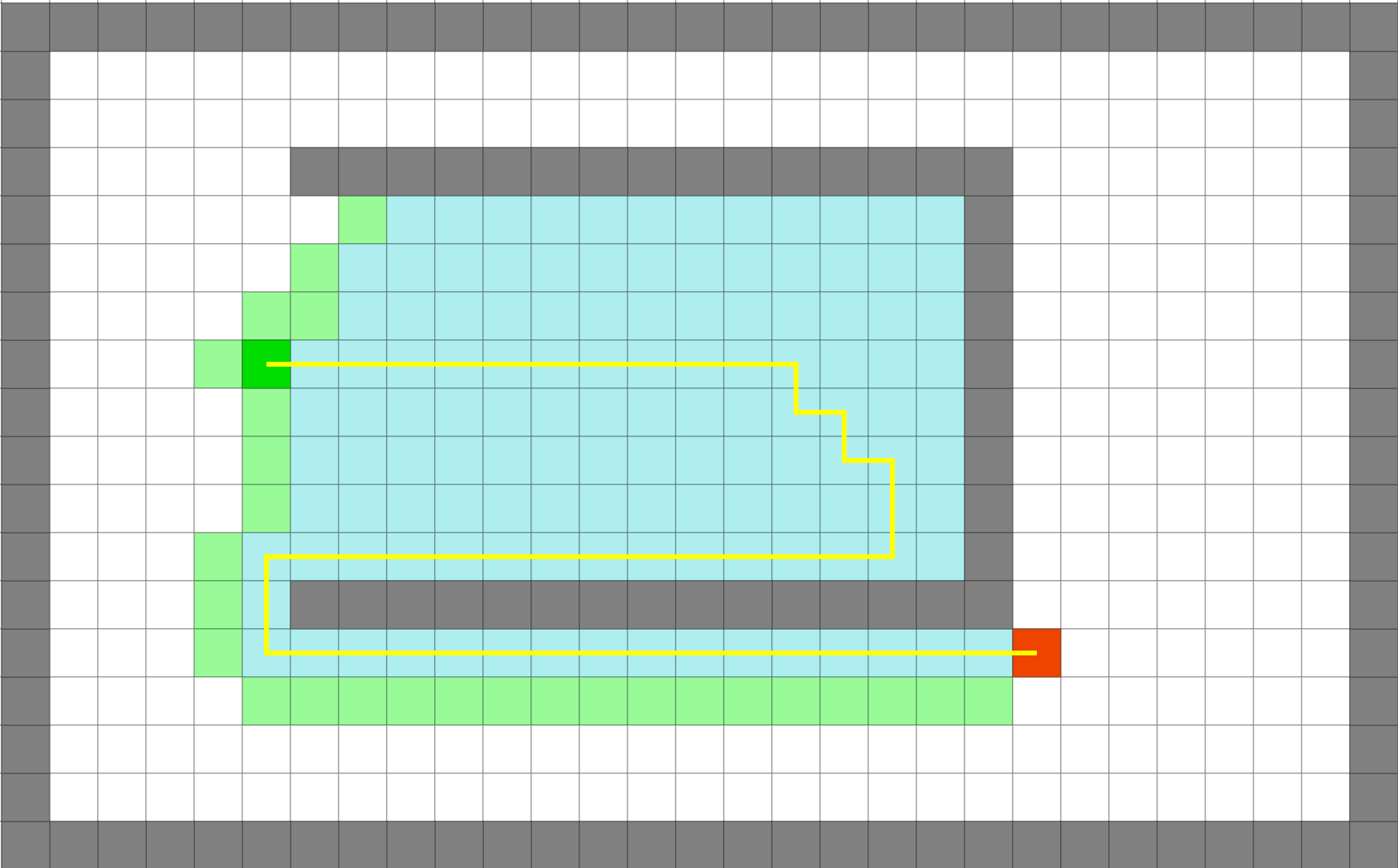
D* (Dynamic A*)
→ 동적인 환경 변화에 대응하여 경로를 탐색할 수 있다.
→ 전체를 계산하지 않고, 변화가 생긴 지점부터 주변으로 상태를 전파하여 경로를 갱신한다.
→ 많은 메모리가 필요함. -
D* lite
→ 동적인 환경에서 효율적으로 경로를 재탐색하기 위해 만들어졌다.
→ LPA* 의 응용버전
→ D의 간단한 버전은 아니지만 D 보다 구현이 쉬워 Lite가 붙었다고한다.